Gegenseitige Lage von zwei Geraden

Stell dir vor, du hast zwei Geraden im Raum - wie verhalten sie sich zueinander? Es gibt genau vier Möglichkeiten, die du systematisch unterscheiden kannst.

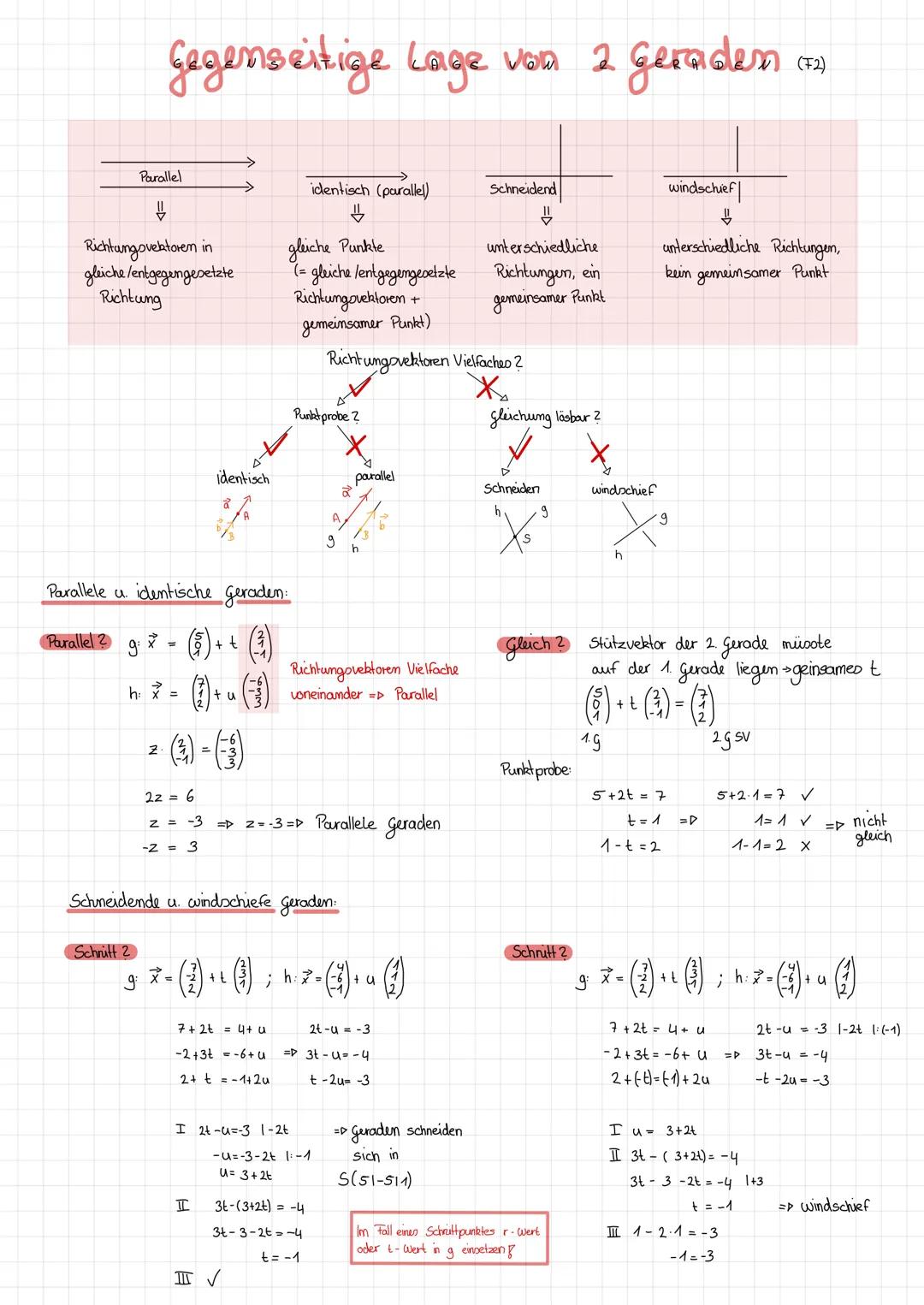
Parallel bedeutet, dass die Richtungsvektoren Vielfache voneinander sind, aber die Geraden keinen gemeinsamen Punkt haben. Identisch sind Geraden, wenn sie dieselben Richtungsvektoren haben UND einen gemeinsamen Punkt besitzen - sie sind also deckungsgleich.

Bei schneidenden Geraden haben die Richtungsvektoren unterschiedliche Richtungen, aber es gibt genau einen gemeinsamen Schnittpunkt. Windschiefe Geraden findest du nur im dreidimensionalen Raum - sie haben unterschiedliche Richtungen und keinen gemeinsamen Punkt.

Tipp: Prüfe immer zuerst die Richtungsvektoren, dann machst du eine Punktprobe!

Das Beispiel zeigt dir den praktischen Ablauf: Erst checkst du, ob die Richtungsvektoren Vielfache sind $hier: Vektor (2,1) und (-1,-3) sind es nicht$. Dann setzt du die Geradengleichungen gleich und löst das Gleichungssystem. Ist es lösbar, schneiden sich die Geraden - ist es unlösbar, sind sie windschief.