Mathematik

Flächenberechnungsmethoden mit Integralen

Integral

2,055

•

Aktualisiert Mar 16, 2026

•

4 Seiten

Integralrechnung - Einfach erklärt und Lernzettel

mia

@mia.ldf

Integralrechnung ist ein zentrales Thema der Oberstufen-Mathematik, das dir zeigt,... Mehr anzeigen

1 / 4

$# Mathe GK Klausur- integral pobere Grenze (rechts) $ \int_{a}^{b} f(x)dx = [F(x)]_{a}^{b} \rightarrow Stammfunktion $ Guntere Grenze (u$

Grundlagen der Integralrechnung

Das Integralzeichen ∫ steht für "Summe" und zeigt dir, dass du Flächen zwischen einem Graphen und der x-Achse berechnest. Du schreibst es als ∫ₐᵇ f(x)dx, wobei a die untere Grenze (links) und b die obere Grenze (rechts) ist.

Das Coole dabei: Das Integral berücksichtigt orientierte Flächeninhalte. Liegt die Funktion über der x-Achse, ist die Fläche positiv - liegt sie darunter, wird sie negativ gezählt. So ergibt sich: ∫ₐᵇ f(x)dx = A₁ - A₂ + A₃ - A₄.

Um Integrale zu verstehen, hilft die Vorstellung von Ober- und Untersummen. Du näherst die Fläche durch Rechtecke an - die Untersumme ist immer kleiner, die Obersumme immer größer als der wahre Wert. Je mehr Rechtecke du verwendest, desto genauer wird deine Annäherung.

Merktipp: Das Integral liegt immer zwischen Ober- und Untersumme - wie ein Sandwich!

$# Mathe GK Klausur- integral pobere Grenze (rechts) $ \int_{a}^{b} f(x)dx = [F(x)]_{a}^{b} \rightarrow Stammfunktion $ Guntere Grenze (u$

Stammfunktionen und der Hauptsatz

Eine Stammfunktion F(x) ist das Gegenteil der Ableitung: Wenn F'(x) = f(x), dann ist F eine Stammfunktion von f. Mit ihr kannst du Integrale super einfach berechnen, ohne mühsam Rechtecke zu zählen.

Der Hauptsatz der Differential- und Integralrechnung besagt: ∫ₐᵇ f(x)dx = F(b) - F(a). Du setzt also die obere Grenze in die Stammfunktion ein, ziehst die untere Grenze ab - fertig!

Die wichtigsten Aufleitungsregeln sind easy: Bei xⁿ wird's zu $1/(n+1)$ ·xⁿ⁺¹ (Potenzregel). Summen bleiben Summen (Summenregel), und Konstanten bleiben vor dem Integral stehen (Faktorregel).

Integrale haben mega praktische Anwendungen: Aus der Geschwindigkeit kriegst du die Wegstrecke, aus der Wachstumsrate den Zuwachs, aus der Wasserzuflussstärke die gesamte Wassermenge.

Praxis-Tipp: Stammfunktionen sind wie das Rückwärtsfahren beim Ableiten - einfach die Regeln umdrehen!

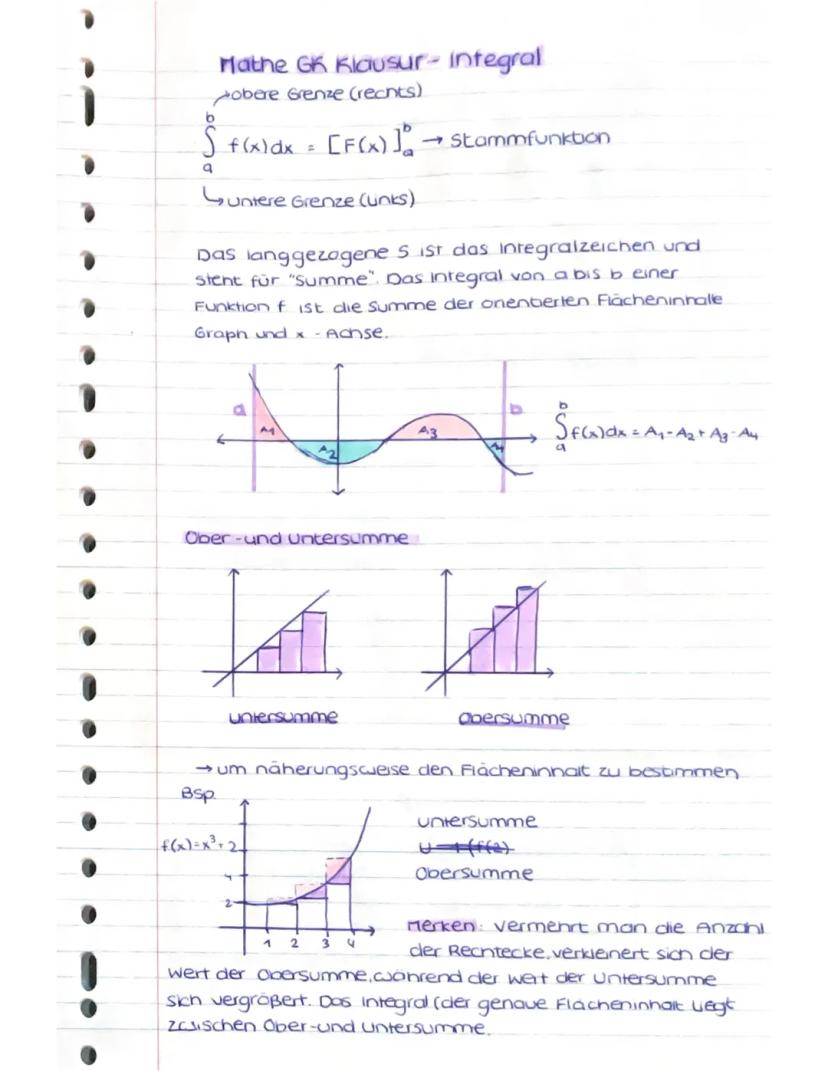
$# Mathe GK Klausur- integral pobere Grenze (rechts) $ \int_{a}^{b} f(x)dx = [F(x)]_{a}^{b} \rightarrow Stammfunktion $ Guntere Grenze (u$

Rechenregeln und Flächenberechnungen

Mit den Rechenregeln für Integrale sparst du dir viel Arbeit. Wenn beide Grenzen gleich sind, ist das Integral null. Vertauschst du die Grenzen, ändert sich nur das Vorzeichen. Das Integral ist linear - das bedeutet, du kannst Summen aufteilen und Konstanten rausziehen.

Den Flächeninhalt zwischen zwei Graphen berechnest du mit ∫ₐᵇ $f(x) - g(x)$ dx. Dabei ist egal, auf welcher Höhe die Funktionen liegen - der Abstand bleibt gleich. Du kannst auch erst beide Integrale einzeln berechnen und dann subtrahieren.

Bei komplexeren Aufgaben kombinierst du verschiedene Techniken. Manchmal musst du Gesamtflächen berechnen und dann Teilflächen (wie Kreise) abziehen. Das Prinzip bleibt immer gleich: A = A_Gesamt - A_Teil.

Trick: Zeichne dir die Situation immer auf - so siehst du sofort, welche Flächen du brauchst!

$# Mathe GK Klausur- integral pobere Grenze (rechts) $ \int_{a}^{b} f(x)dx = [F(x)]_{a}^{b} \rightarrow Stammfunktion $ Guntere Grenze (u$

Mittelwerte berechnen

Den Mittelwert einer Funktion über ein Intervall findest du mit der Formel: m̄ = $1/(b-a)$ ∫ₐᵇ f(x)dx. Das ist wie bei normalen Durchschnittswerten, nur dass du unendlich viele Werte hast.

Du kannst die Formel auch als m̄ = (∫ₐᵇ f(x)dx)/ $b-a$ schreiben - das ist dasselbe, nur anders angeordnet. Nimm einfach die Version, die dir besser gefällt.

Der Mittelwert ist super praktisch für reale Probleme: durchschnittliche Geschwindigkeit, mittlere Temperatur über einen Tag oder durchschnittlicher Wasserverbrauch.

Eselsbrücke: Mittelwert = Integral geteilt durch Intervallbreite - ganz logisch!

Wir dachten schon, du fragst nie...

Was ist der Knowunity KI-Begleiter?

Unser KI-Begleiter ist ein speziell für Schüler entwickeltes KI-Tool, das mehr als nur Antworten bietet. Basierend auf Millionen von Knowunity-Inhalten liefert er relevante Informationen, personalisierte Lernpläne, Quizze und Inhalte direkt im Chat und passt sich deinem individuellen Lernweg an.

Wo kann ich die Knowunity-App herunterladen?

Du kannst die App im Google Play Store und im Apple App Store herunterladen.

Ist Knowunity wirklich kostenlos?

Genau! Genieße kostenlosen Zugang zu Lerninhalten, vernetze dich mit anderen Schülern und hol dir sofortige Hilfe – alles direkt auf deinem Handy.

Beliebtester Inhalt: Integral

Analyse und Funktionen

Umfassende Zusammenfassung für das ABI zur Analysis. Behandelt werden: verschiedene Funktionstypen, Funktionsscharen, Differentialrechnung, Kurvendiskussion, Extremwertaufgaben und Integralrechnung. Ideal für Schüler, die sich auf Prüfungen vorbereiten.

Integralrechnung - Einfach erklärt und Lernzettel

Grundlagen der Integralrechnung

Stammfunktionen und der Hauptsatz

Rechenregeln und Flächenberechnungen

Mittelwerte berechnen

Wir dachten schon, du fragst nie...

Was ist der Knowunity KI-Begleiter?

Wo kann ich die Knowunity-App herunterladen?

Ist Knowunity wirklich kostenlos?

Ähnlicher Inhalt