Kombinatorik - Die Kunst des Zählens

Kombinatorik hilft dir dabei herauszufinden, wie viele verschiedene Möglichkeiten es bei bestimmten Situationen gibt. Die Grundfrage ist immer: Kommt es auf die Reihenfolge an und dürfen sich Elemente wiederholen?

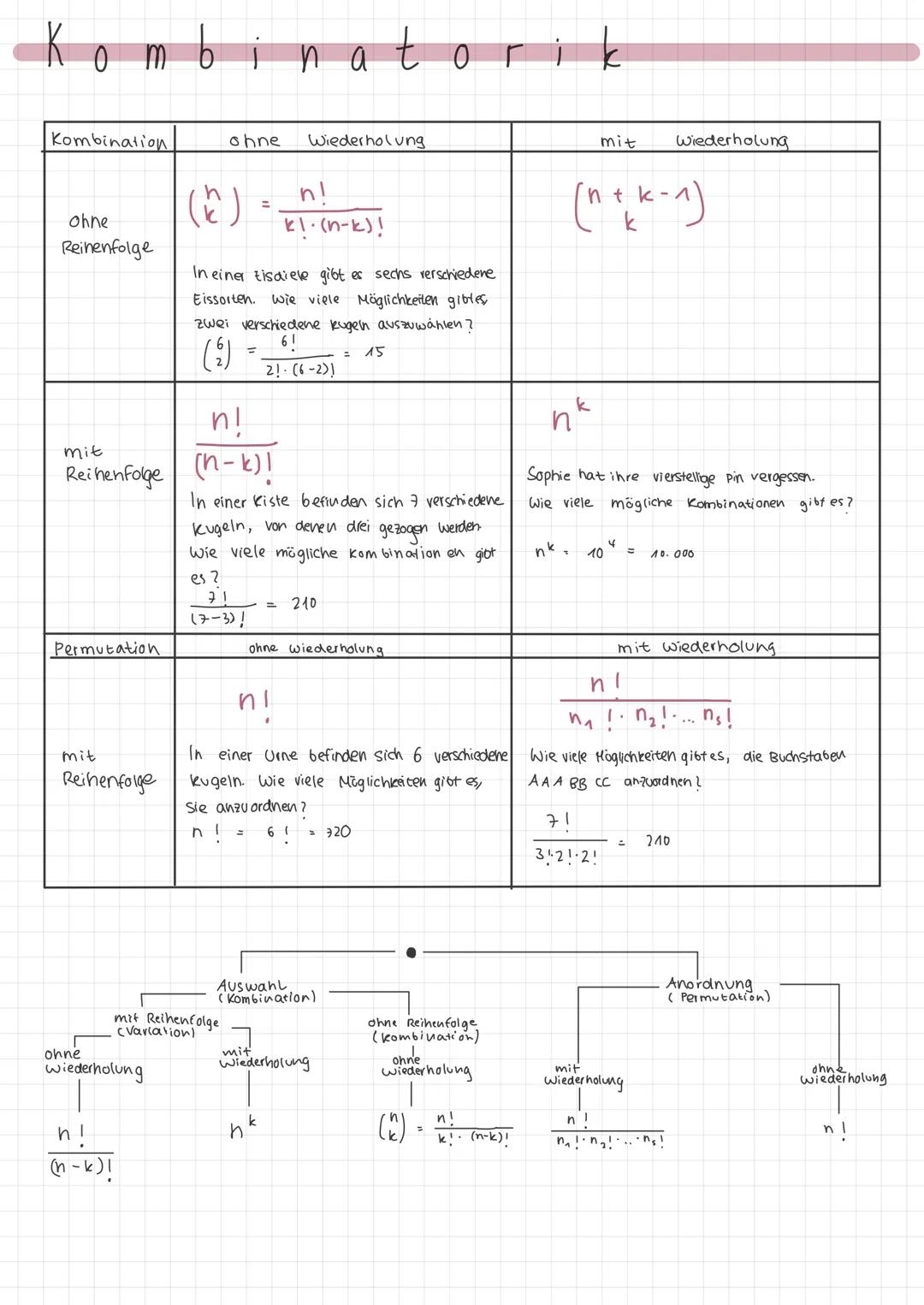
Bei Kombinationen ohne Wiederholung (wie bei der Eisauswahl mit 6 Sorten für 2 verschiedene Kugeln) verwendest du die Formel $\binom{n}{k} = \frac{n!}{k!(n-k)!}$. Das ergibt hier 15 Möglichkeiten, weil die Reihenfolge egal ist.

Wenn die Reihenfolge wichtig ist, sprichst du von Variationen. Ohne Wiederholung nutzt du $\frac{n!}{(n-k)!}$ - wie bei den 7 Kugeln, von denen 3 gezogen werden (240 Möglichkeiten). Mit Wiederholung ist es noch einfacher: $n^k$, wie bei Sophies vierstelliger PIN mit 10.000 Möglichkeiten.

Merktipp: Frage dich immer zuerst: "Ist die Reihenfolge wichtig?" und "Dürfen sich Elemente wiederholen?"

Permutationen beschäftigen sich mit Anordnungen. Ohne Wiederholung sind das einfach $n!$ Möglichkeiten (6 Kugeln = 720 Anordnungen). Bei gleichen Elementen teilst du durch die Fakultäten der gleichen Objekte: $\frac{n!}{n_1! n_2! ... n_s!}$.