Lineare Funktionen verstehen und berechnen
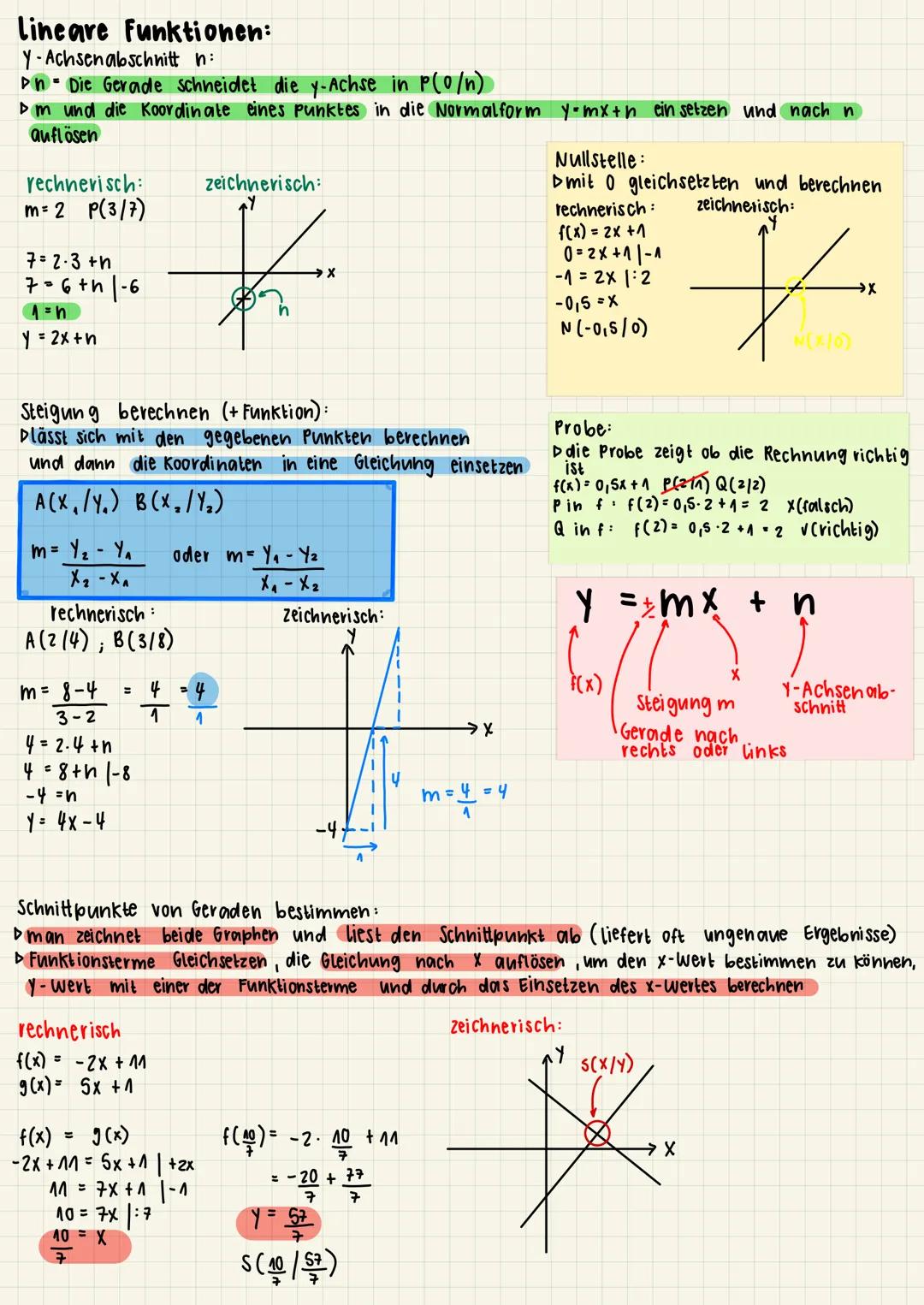
Jede lineare Funktion hat die Form y = mx + n, wobei m die Steigung und n der Y-Achsenabschnitt ist. Der Y-Achsenabschnitt n ist der Punkt, an dem die Gerade die y-Achse schneidet: P0/n.
Um den Y-Achsenabschnitt zu berechnen, kannst du einen bekannten Punkt und die Steigung in die Normalform einsetzen. Zum Beispiel: Bei m=2 und P(3/7) rechnest du 7 = 2 · 3 + n, also n = 1.
Die Nullstelle einer Funktion findest du, indem du die Funktion mit 0 gleichsetzt. Bei f(x) = 2x + 1 rechnest du: 0 = 2x + 1, daraus folgt x = -0,5. Die Nullstelle liegt also bei N(-0,5/0).
💡 Tipp: Denk daran, dass die Nullstelle immer auf der x-Achse liegt - der y-Wert ist immer 0!
Zur Berechnung der Steigung zwischen zwei Punkten Ax1/y1 und Bx2/y2 verwendest du die Formel:
m = y2−y1/x2−x1
Schnittpunkte zwischen zwei Geraden findest du, indem du die Funktionsterme gleichsetzt. Löse die Gleichung nach x auf und berechne dann den zugehörigen y-Wert. Zum Beispiel: Bei f(x) = -2x + 11 und g(x) = 5x + 1 setzt du -2x + 11 = 5x + 1, löst nach x auf und erhältst x = 10/7 und y = 50/7.
Mache immer eine Probe, um dein Ergebnis zu überprüfen! Setze dafür die gefundenen Koordinaten in die ursprüngliche Funktion ein.