Lineare Gleichungen mit 2 Variablen
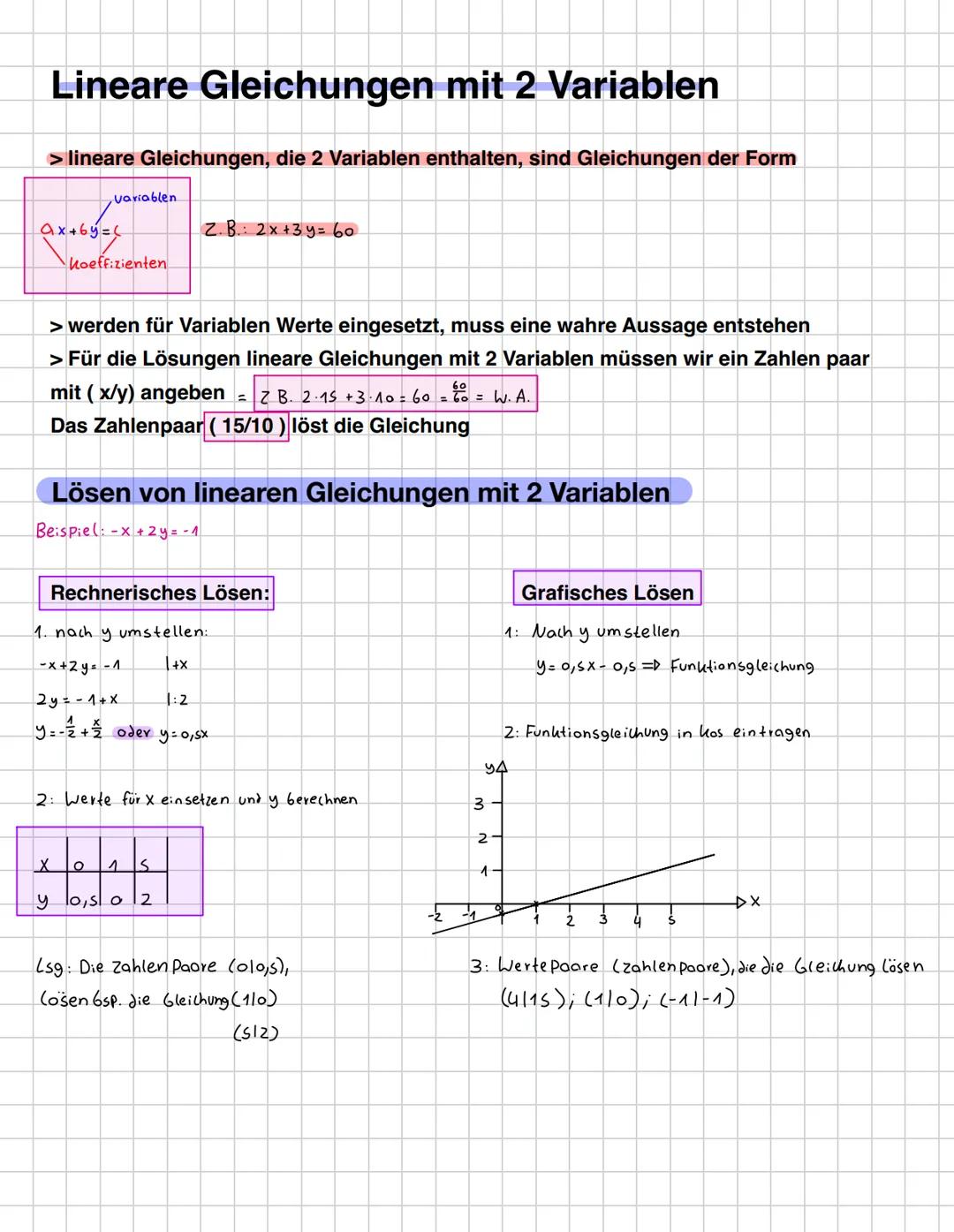
Lineare Gleichungen mit zwei Unbekannten haben immer die Form Ax + By = C. Ein typisches Beispiel ist 2x + 3y = 60, wo A, B und C die Koeffizienten sind.
Die Lösung einer solchen Gleichung ist immer ein Zahlenpaar (x|y). Wenn du diese Werte einsetzt, muss eine wahre Aussage entstehen. Zum Beispiel löst das Zahlenpaar (15|10) die Gleichung 2x + 3y = 60, weil 2·15 + 3·10 = 60 stimmt.
Es gibt zwei Hauptmethoden zum Lösen: rechnerisch und grafisch. Beide Wege führen dich zu den gleichen Lösungen, aber der grafische Weg zeigt dir die Lösungen als Punkte auf einer Geraden.
Tipp: Jede lineare Gleichung mit zwei Variablen hat unendlich viele Lösungen - alle Punkte auf der zugehörigen Geraden!
Beim rechnerischen Lösen stellst du zuerst nach y um: Aus -x + 2y = -4 wird y = 0,5x - 2. Dann setzt du verschiedene x-Werte ein und berechnest die passenden y-Werte. So erhältst du Zahlenpaare wie (0|-2), (2|-1) oder (4|0).
Für das grafische Lösen trägst du die Funktionsgleichung y = 0,5x - 2 in ein Koordinatensystem ein. Alle Punkte auf dieser Geraden sind Lösungen der ursprünglichen Gleichung.