Erweiterte Lösungsmethoden
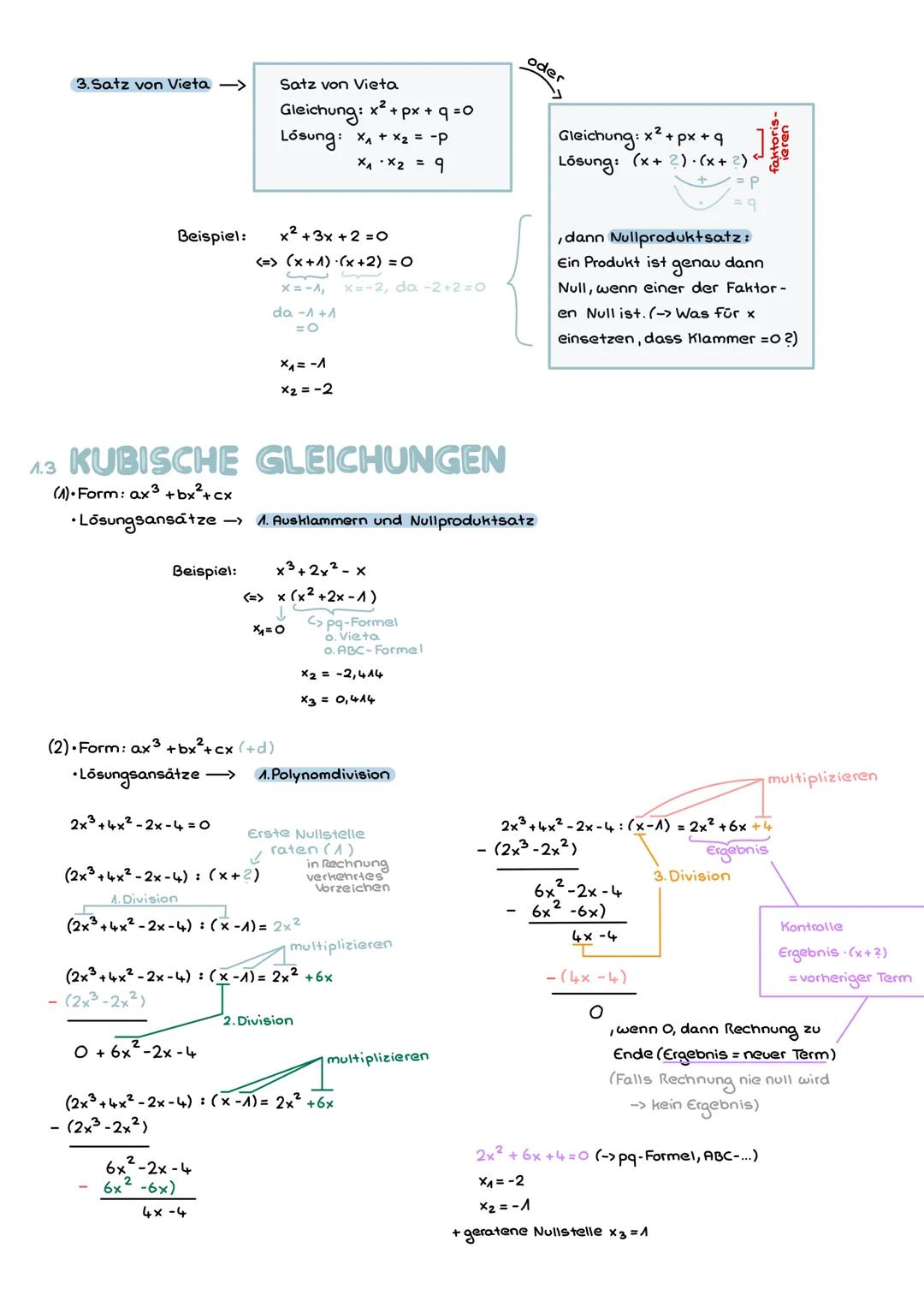
Der Satz von Vieta ist super praktisch, wenn du die Lösungen einer quadratischen Gleichung schon kennst oder raten kannst. Bei x² + px + q = 0 gilt: x₁ + x₂ = -p und x₁ · x₂ = q. Das hilft dir oft beim Faktorisieren.
Wenn du faktorisieren kannst, verwendest du den Nullproduktsatz: Ein Produkt ist null, wenn mindestens ein Faktor null ist. Bei x+1x+2 = 0 setzt du beide Klammern gleich null.
Kubische Gleichungen sind schon eine andere Liga, aber keine Panik! Bei x³ + 2x² - x = 0 klammerst du erst x aus: xx2+2x−1 = 0. Dann hast du sofort eine Lösung x=0 und eine quadratische Gleichung übrig.
Wichtig: Bei kubischen Gleichungen mit konstantem Term wie2x3+4x2−2x−4=0 brauchst du die Polynomdivision!
Für die Polynomdivision rätst du zuerst eine Nullstelle (probiere ±1, ±2, etc. aus). Dann teilst du das Polynom durch x−gerrateneNullstelle und bekommst eine quadratische Gleichung, die du normal lösen kannst.