Analysis - Grundlagen

Analysis ist das mathematische Werkzeug, mit dem du Funktionen verstehst und untersuchst. Du lernst hier, wie sich Funktionen verhalten, wo sie ihre Höhe- und Tiefpunkte haben und wie schnell sie wachsen.

Das Coole daran: Mit diesen Methoden kannst du echte Probleme lösen - von der optimalen Verpackungsgröße bis zur Geschwindigkeitsanalyse von Fahrzeugen. Die Analysis gibt dir die mathematische Sprache, um Veränderungen zu beschreiben und vorherzusagen.

Tipp: Analysis baut aufeinander auf - jede Funktion folgt ähnlichen Untersuchungsschritten!

Lineare Funktionen

Lineare Funktionen sind deine ersten echten Funktionen und folgen der Form f(x) = mx + b. Die Steigung m zeigt dir, wie steil die Gerade verläuft, während b den y-Achsenabschnitt angibt.

Parallele Geraden haben immer die gleiche Steigung. Bei orthogonalen Geraden multiplizierst du die Steigungen und erhältst -1 $m₁ · m₂ = -1$. Den Schnittpunkt mit der x-Achse findest du, indem du f(x) = 0 setzt.

Für Schnittpunkte zweier Geraden setzt du beide Gleichungen gleich und löst nach x auf. Den Steigungswinkel berechnest du mit tan(α) = m.

Merke dir: Orthogonale Geraden stehen senkrecht aufeinander - ihre Steigungen sind negative Kehrwerte!

Quadratische Funktionen

Quadratische Funktionen haben die allgemeine Form f(x) = ax² + bx + c oder die praktische Scheitelpunktform f(x) = a$x-d$² + e. Der Parameter a bestimmt die Öffnungsrichtung: a > 0 nach oben, a < 0 nach unten.

Der Streckfaktor |a| verändert die Parabelbreite: |a| > 1 streckt sie, |a| < 1 staucht sie. Die Parameter d und e verschieben die Parabel horizontal bzw. vertikal.

Mit der p-q-Formel löst du quadratische Gleichungen: x₁/₂ = -p/2 ± √$(p/2)² - q$. Die quadratische Ergänzung hilft dir, von der allgemeinen zur Scheitelpunktform zu wechseln.

Tangenten haben im Berührpunkt die gleiche Steigung wie die Funktion selbst. Die Normale steht senkrecht zur Tangente.

Praxis-Tipp: Die Scheitelpunktform zeigt dir sofort den höchsten oder tiefsten Punkt der Parabel!

Trigonometrische Funktionen

Die Sinus- und Kosinusfunktionen sind periodische Funktionen mit der allgemeinen Form f(x) = a·sin$b(x+c)$ + d. Dabei streckt a in y-Richtung, b in x-Richtung, c verschiebt horizontal und d vertikal.

sin(x) ist punktsymmetrisch zum Ursprung, cos(x) ist achsensymmetrisch zur y-Achse. Beide Funktionen schwingen zwischen -1 und +1.

Für die Umrechnung zwischen Gradmaß und Bogenmaß verwendest du: x = (α/360°) · 2π bzw. α = $x/2π$ · 360°. Das Bogenmaß ist besonders praktisch für Ableitungen.

Die Ableitungen sind besonders elegant: sin(x) wird zu cos(x), cos(x) wird zu -sin(x).

Wichtig: Trigonometrische Funktionen beschreiben alle wellenartigen Bewegungen - von Schallwellen bis zu Pendeln!

Potenzfunktionen und Ganzrationale Funktionen

Potenzfunktionen f(x) = ax^n unterteilen sich in Parabeln (positiver Exponent) und Hyperbeln (negativer Exponent). Gerade Exponenten erzeugen achsensymmetrische, ungerade Exponenten punktsymmetrische Graphen.

Wurzelfunktionen folgen der Form f(x) = ⁿ√$x-d$ + e und sind streng monoton steigend. Sie verlaufen durch die Punkte (0|0) und (1|1).

Ganzrationale Funktionen haben die Form f(x) = aₙx^n + aₙ₋₁x^$n-1$ + ... + a₁x + a₀. Der Grad n bestimmt die maximale Anzahl der Nullstellen und die maximale Anzahl der Extrempunkte $n-1$.

Das Randverhalten wird vom Leitkoeffizienten und dem höchsten Exponenten bestimmt.

Faustregel: Je höher der Grad, desto "wilder" kann die Funktion aussehen!

Exponentialfunktionen

Exponentialfunktionen f(x) = a·q^x beschreiben exponentielles Wachstum oder Zerfall. Bei q > 1 hast du Wachstum, bei 0 < q < 1 Zerfall. Der Parameter a ist der Startwert.

Die natürliche Exponentialfunktion f(x) = e^x ist besonders wichtig, weil ihre Ableitung wieder sie selbst ist. Für praktische Probleme verwendest du oft B(t) = B(0)·e^(kt).

Die mittlere Änderungsrate berechnest du mit dem Differenzquotienten: m = $f(b)-f(a)$/$b-a$. Das zeigt dir die durchschnittliche Steigung zwischen zwei Punkten.

Für komplizierte Stammfunktionen wie f(x) = x·e^(2x) verwendest du den Formansatz: Du errätst die Form der Lösung und bestimmst die Parameter durch Ableiten und Vergleichen.

Real-World: Exponentialfunktionen beschreiben Bakterienwachstum, radioaktiven Zerfall und Zinswachstum!

Ableitungs- und Integrationsregeln

Die wichtigsten Ableitungsregeln sind deine mathematischen Werkzeuge: Faktorregel (k·u(x) → k·u'(x)), Potenzregel $x^n → n·x^(n-1)$, Summenregel $u+v → u'+v'$, Produktregel $u·v → u'·v + u·v'$ und Kettenregel (u(v(x)) → u'(v(x))·v'(x)).

Beim Integrieren drehst du den Spieß um: Die Integrationsregeln sind quasi die Umkehrung der Ableitungsregeln. Aus x^n wird $1/(n+1)$·x^$n+1$.

Für komplizierte Funktionen nutzt du partielle Integration oder den Formansatz. Bei der linearen Substitution ersetzt du komplizierte Ausdrücke durch einfachere Variablen.

Merkhilfe: Ableiten macht Funktionen "kleiner", Integrieren macht sie "größer"!

Integralrechnung

Eine Stammfunktion F(x) ist eine Funktion, deren Ableitung f(x) ergibt: F'(x) = f(x). Das bestimmte Integral ∫$a bis b$ f(x)dx berechnet Flächeninhalte zwischen Graph und x-Achse.

Positive Bereiche ergeben positive Integralwerte, negative Bereiche negative Werte. Für echte Flächeninhalte musst du die Beträge der Teilflächen addieren.

Der Hauptsatz der Differential- und Integralrechnung verbindet beide Konzepte: ∫$a bis b$ f(x)dx = F(b) - F(a). Das macht Flächenberechnungen super einfach!

Für Flächen zwischen zwei Graphen berechnest du ∫$a bis b$ |f(x) - g(x)|dx, nachdem du die Schnittpunkte bestimmt hast.

Praktisch: Mit Integralen berechnest du Flächen, Volumina und sogar zurückgelegte Wege!

Rechenregeln für Integrale

Die Rechenregeln für Integrale vereinfachen deine Berechnungen erheblich. Konstante Faktoren ziehst du vor das Integralzeichen: ∫k·f(x)dx = k·∫f(x)dx. Summen integrierst du einzeln: ∫$f(x)+g(x)$dx = ∫f(x)dx + ∫g(x)dx.

Bei vertauschten Integrationsgrenzen ändert sich das Vorzeichen: ∫$b bis a$ f(x)dx = -∫$a bis b$ f(x)dx. Du kannst Integrale auch aufteilen: ∫$a bis c$ f(x)dx = ∫$a bis b$ f(x)dx + ∫$b bis c$ f(x)dx.

Für Flächen zwischen zwei Graphen berechnest du zuerst die Schnittpunkte, dann integrierst du |f(x) - g(x)| über die Teilintervalle. Unbegrenzte Flächen näherst du mit Grenzwerten an.

Tipp: Diese Regeln sparen dir viel Rechenzeit - lerne sie auswendig!

Kurvendiskussion

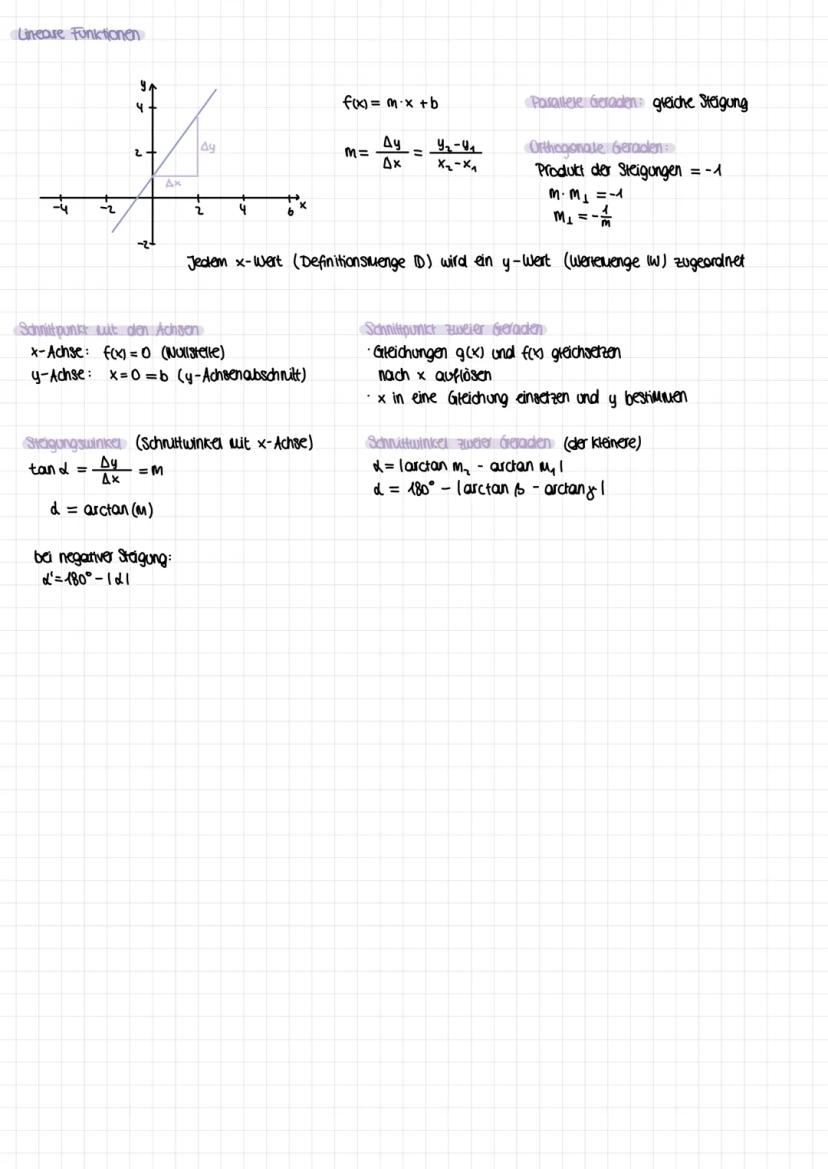
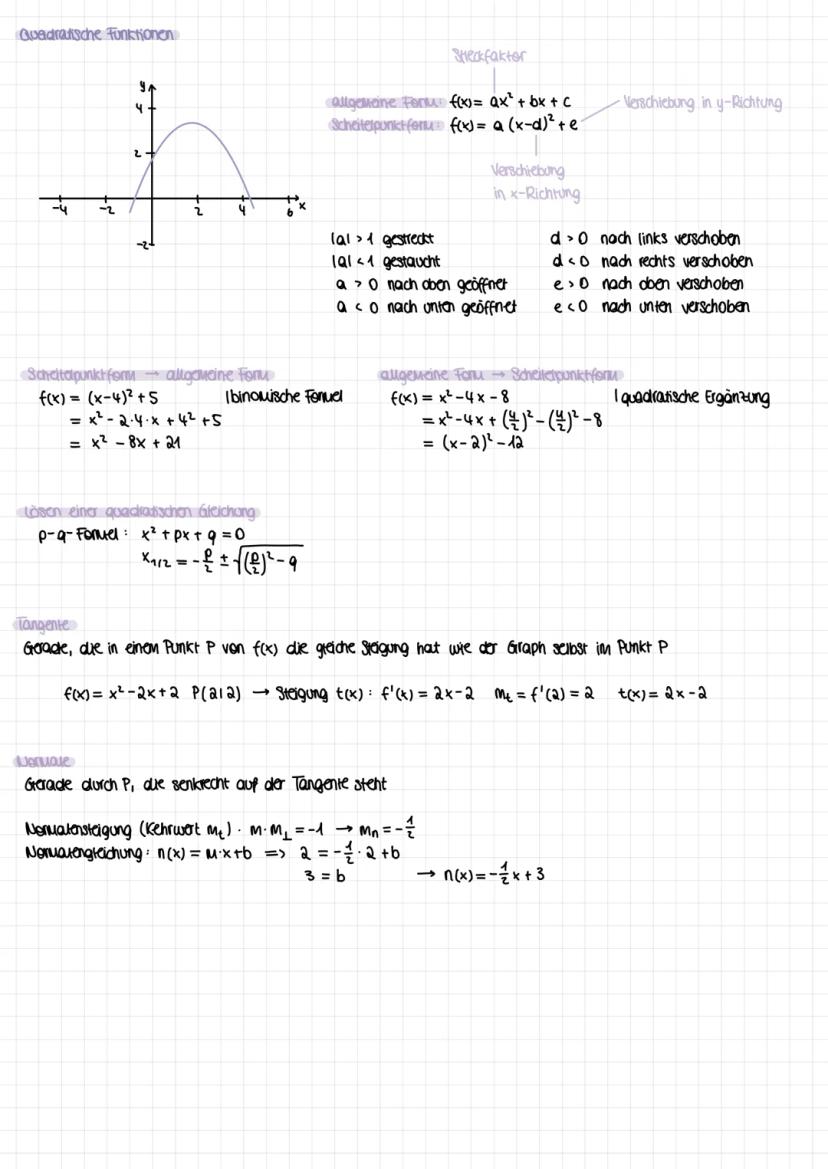
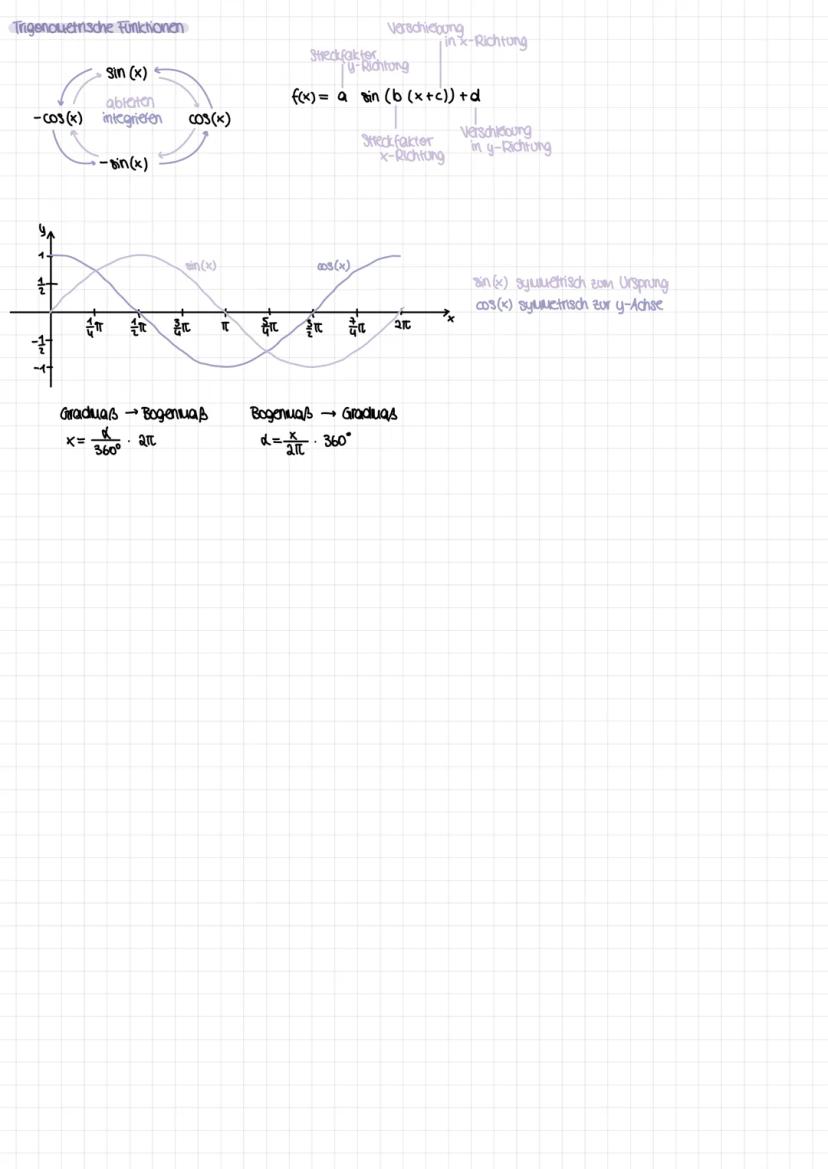
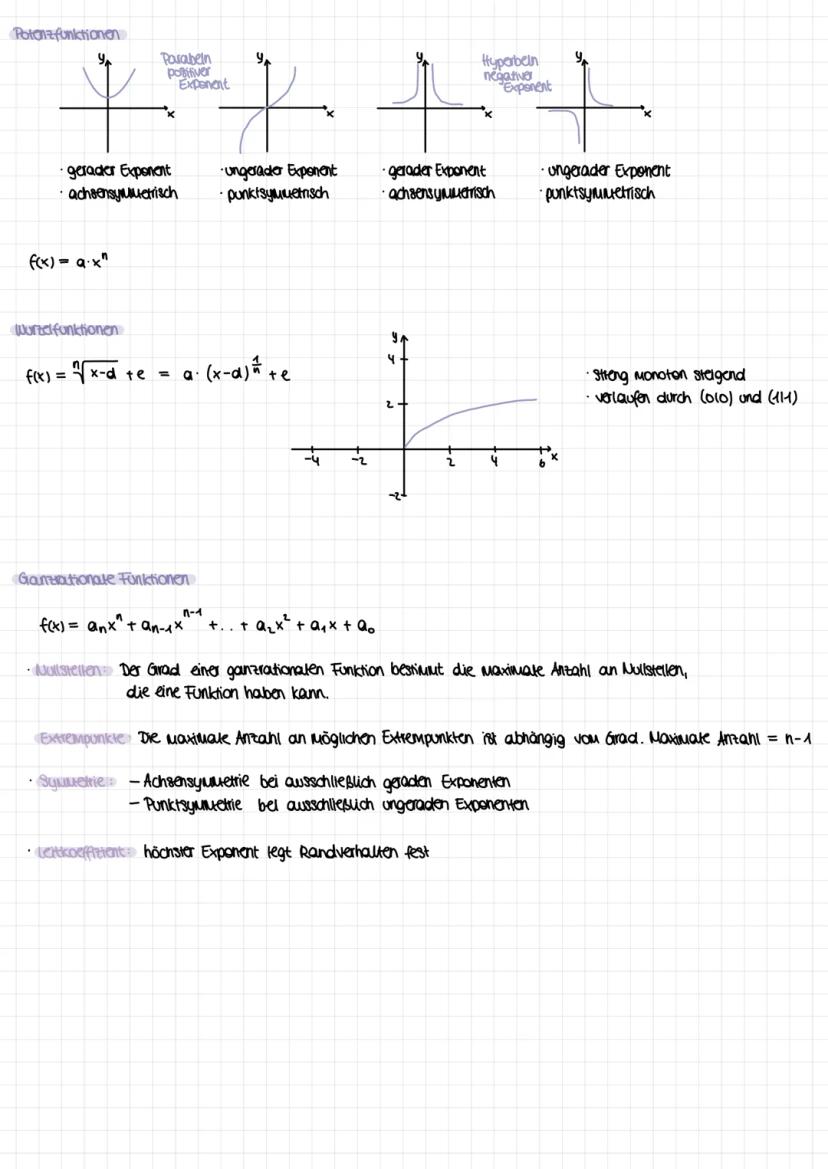
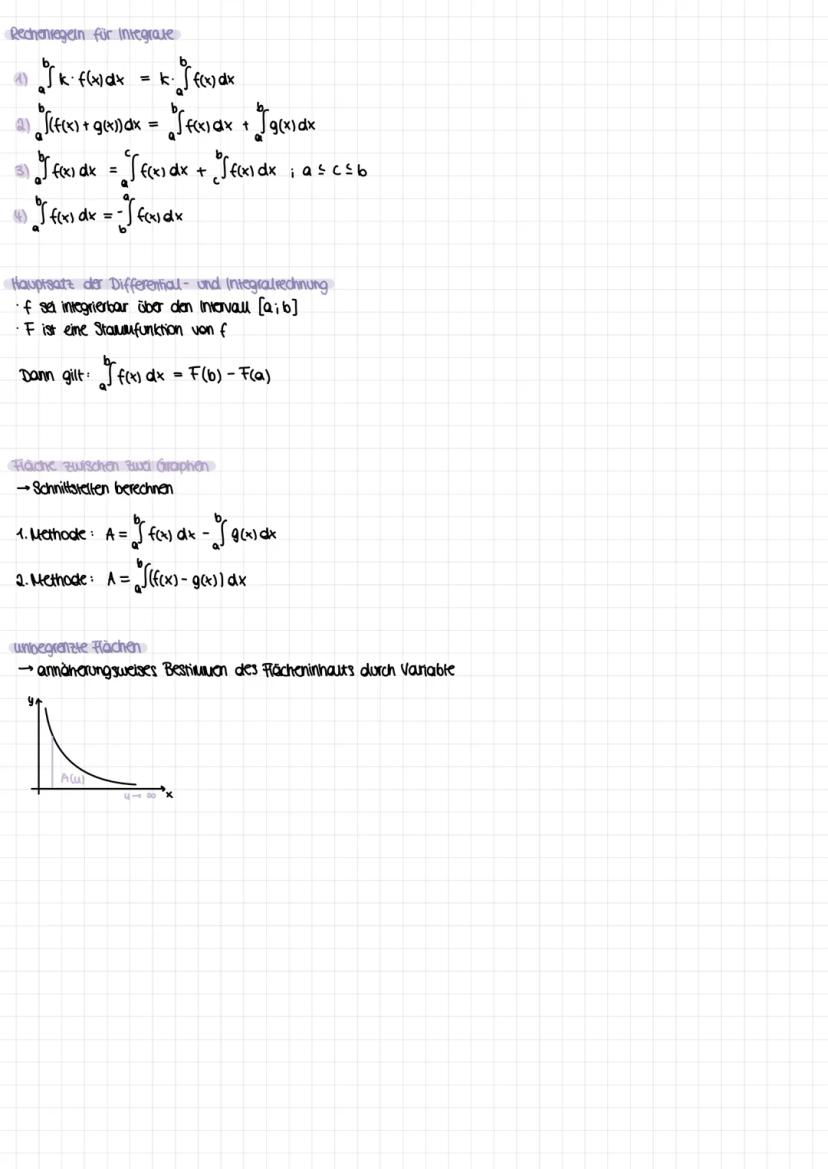
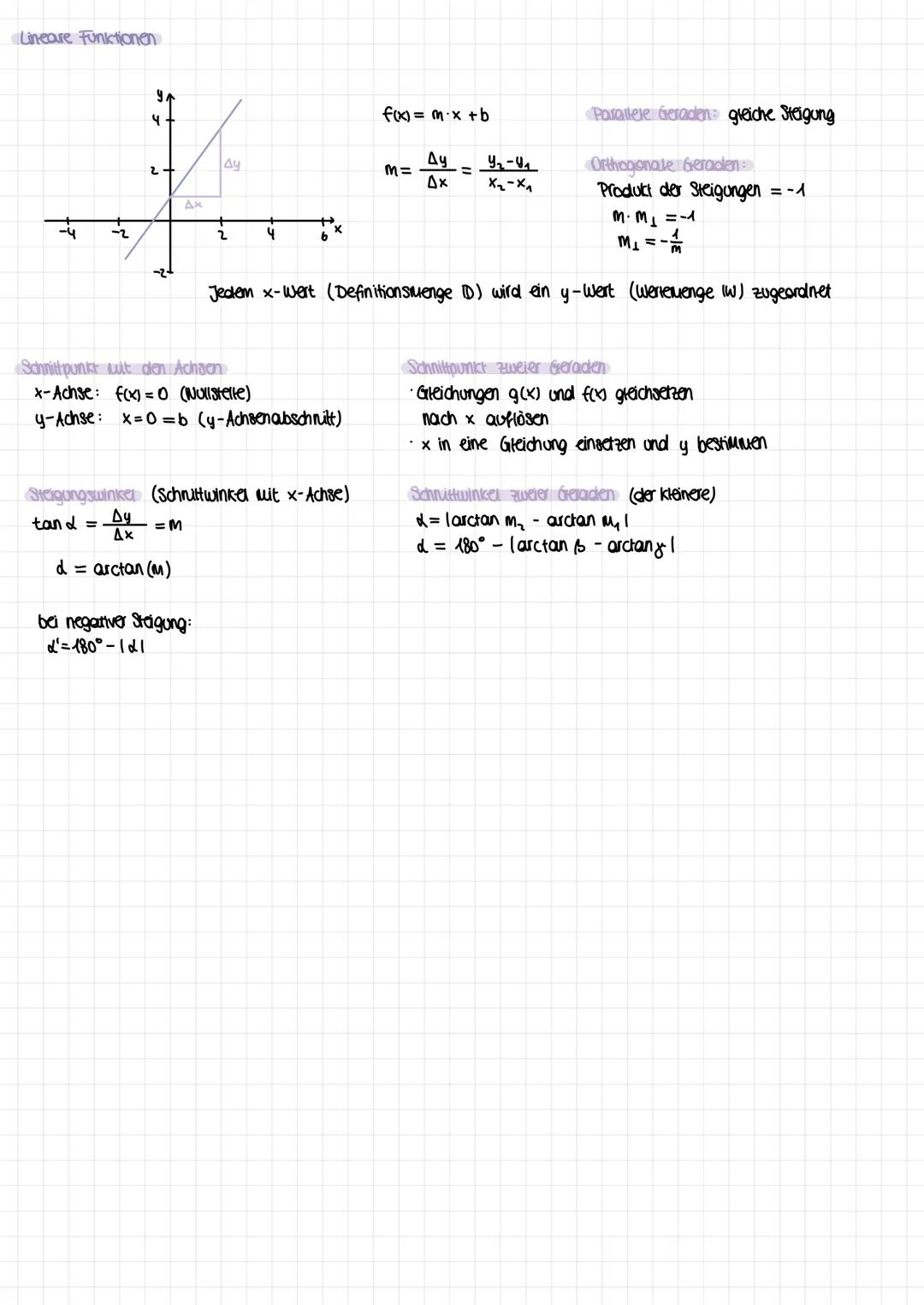
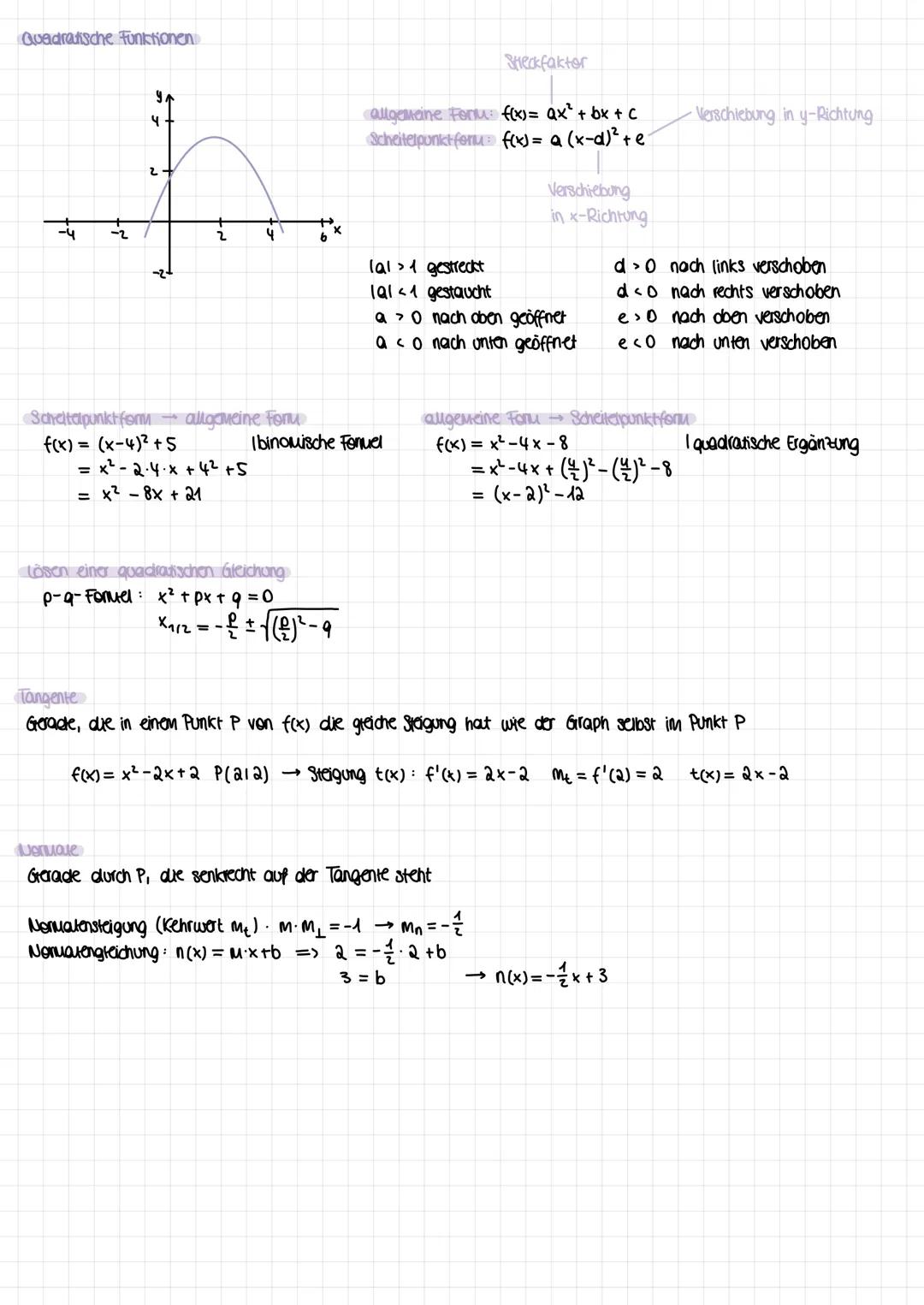
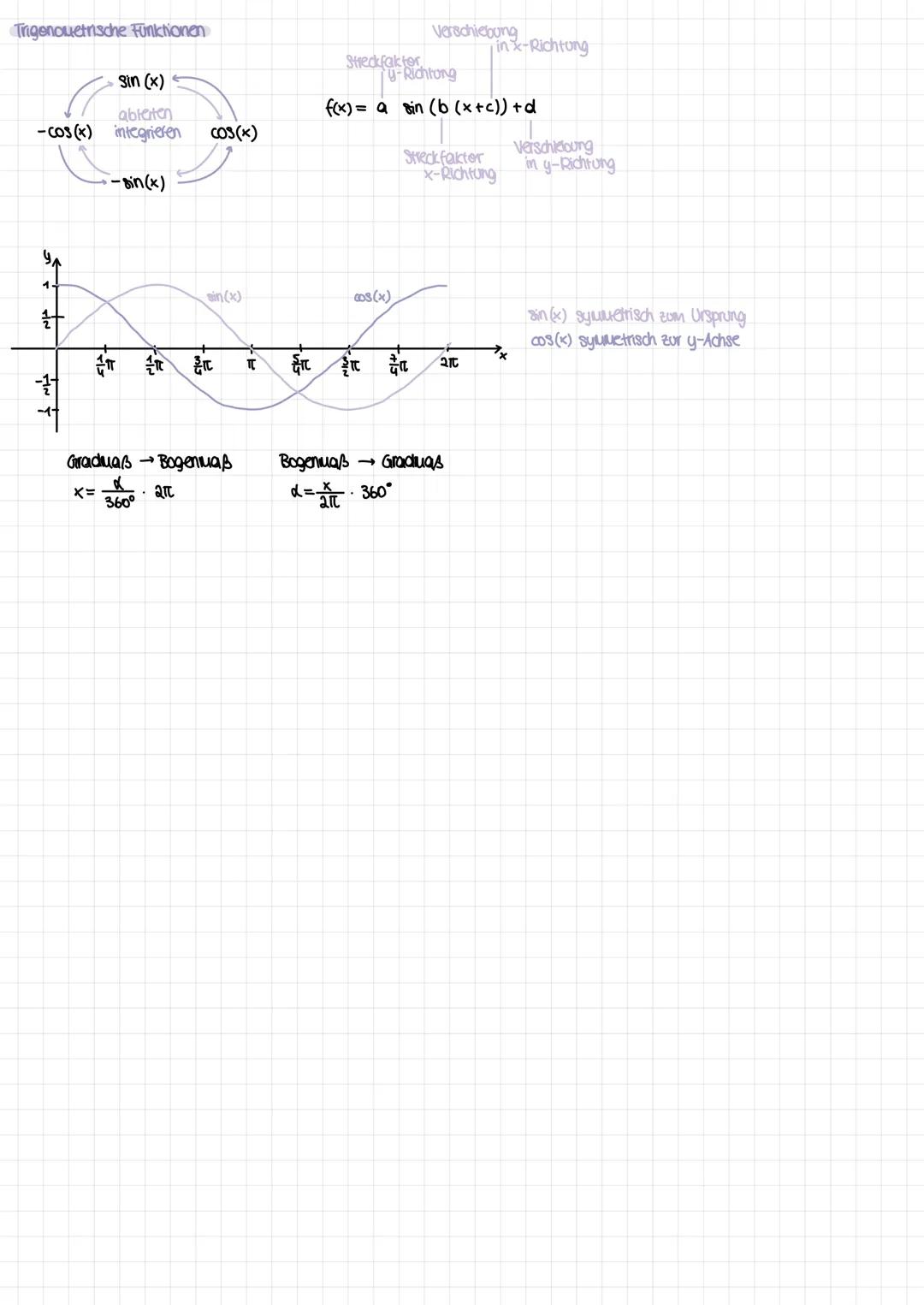
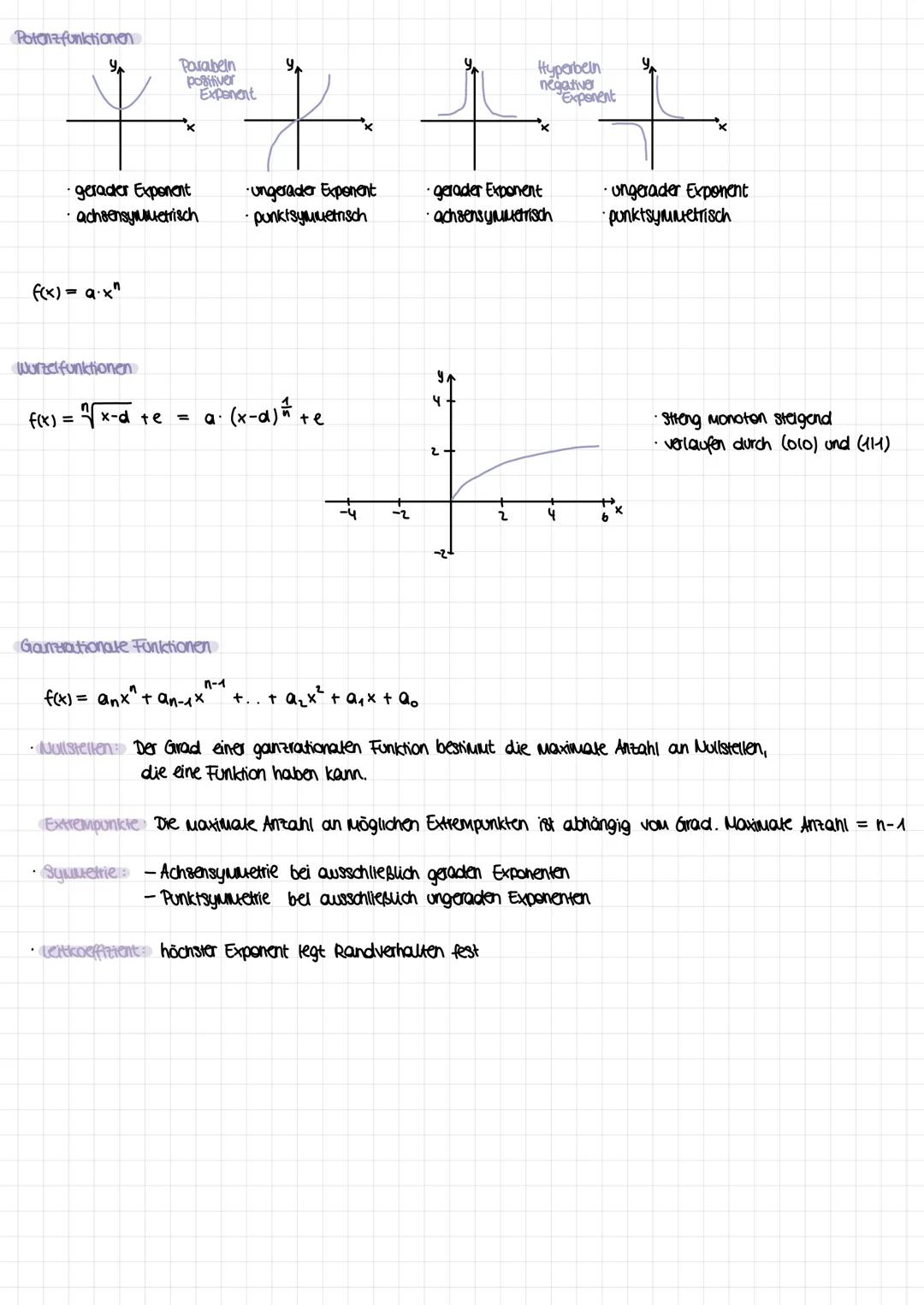
Die Kurvendiskussion ist dein systematisches Vorgehen zur vollständigen Funktionsanalyse. Du untersuchst nacheinander: Definitionsbereich, Symmetrie $f(-x) = f(x) für Achsensymmetrie, f(-x) = -f(x) für Punktsymmetrie$, Randverhalten mit Grenzwerten.

Für Extremstellen suchst du Stellen mit f'(x) = 0 (notwendige Bedingung) und prüfst mit f''(x) ≠ 0 (hinreichende Bedingung). Bei f''(x) > 0 hast du ein Minimum, bei f''(x) < 0 ein Maximum.

Wendepunkte findest du mit f''(x) = 0 und f'''(x) ≠ 0. Das Vorzeichenwechselkriterium hilft dir bei schwierigen Fällen: Wechselt f'(x) von + nach -, hast du einen Hochpunkt.

Die Kurvendiskussion gibt dir das vollständige Bild einer Funktion - perfekt für Klausuraufgaben!

Systematik ist alles: Arbeite immer in derselben Reihenfolge, dann vergisst du nichts!