Potenzfunktionen verstehen
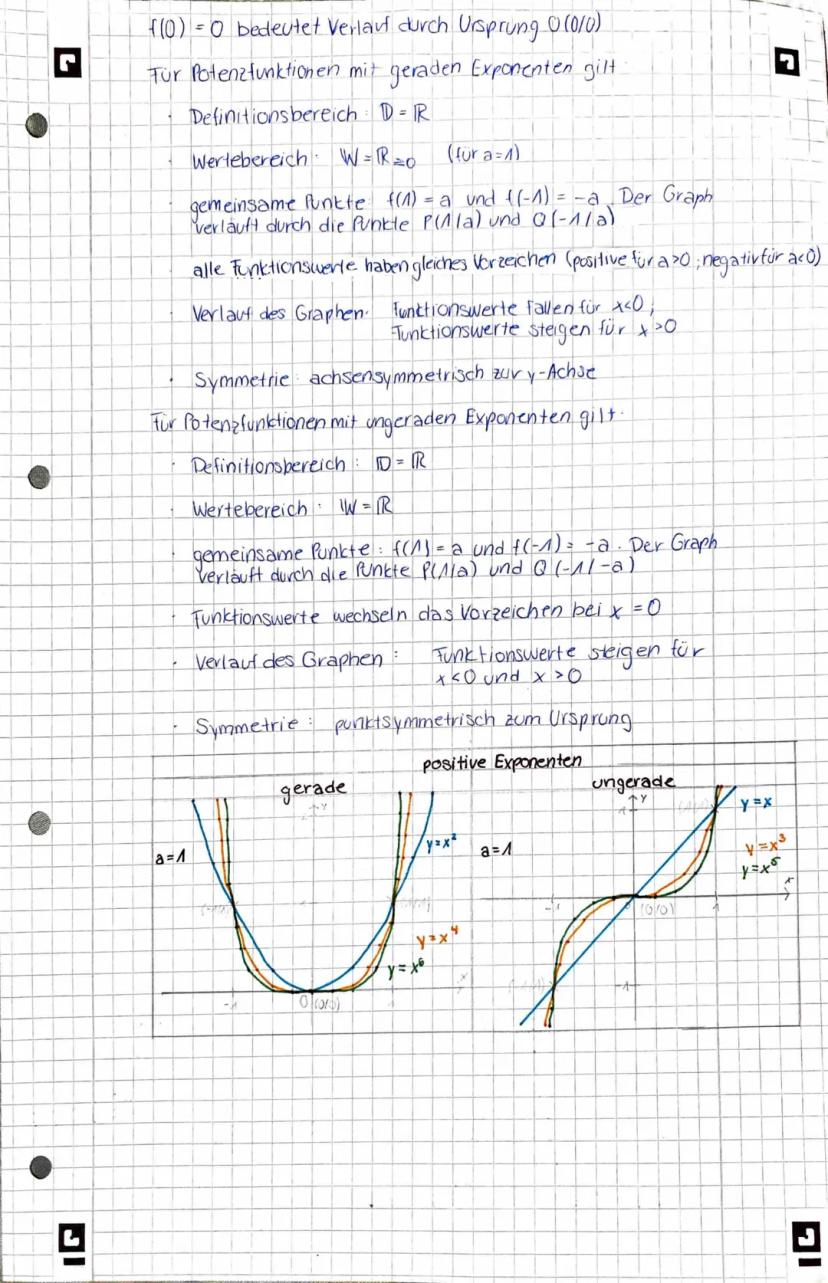
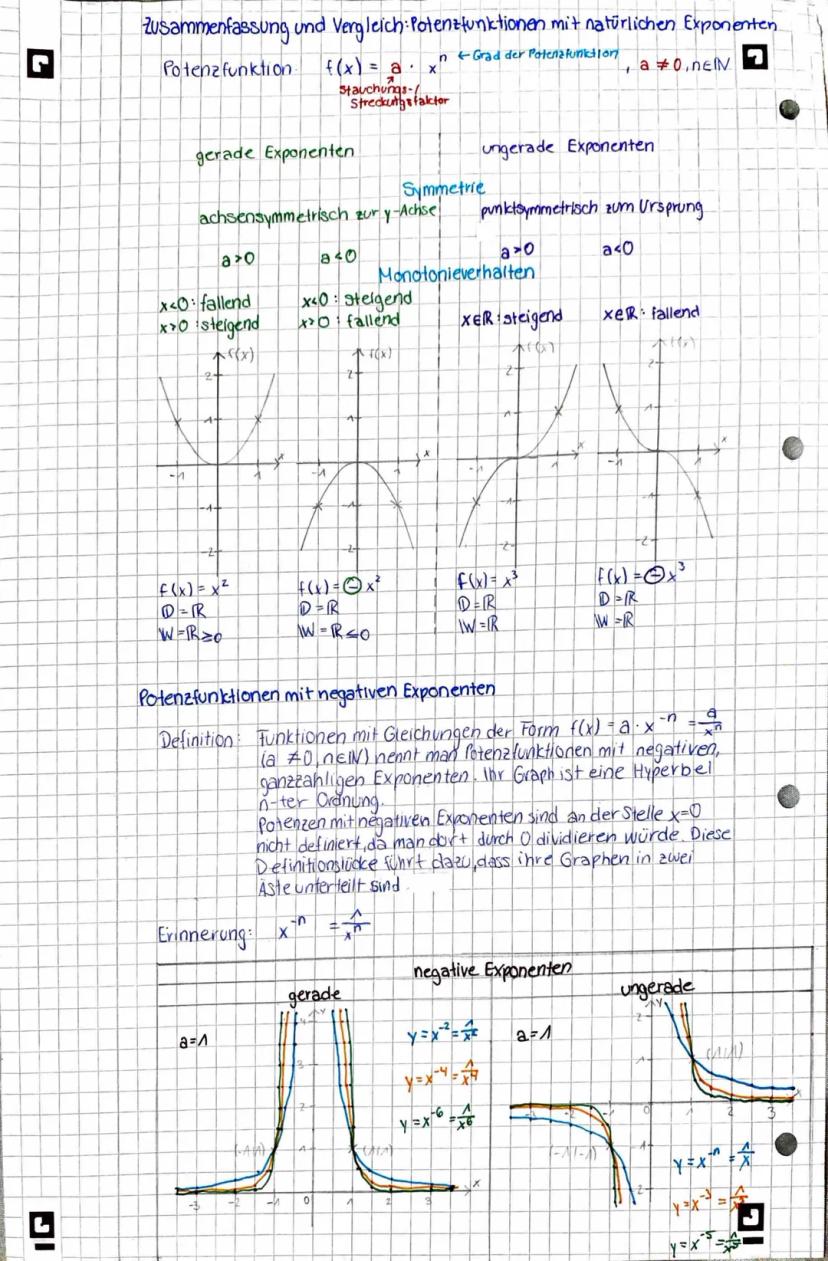
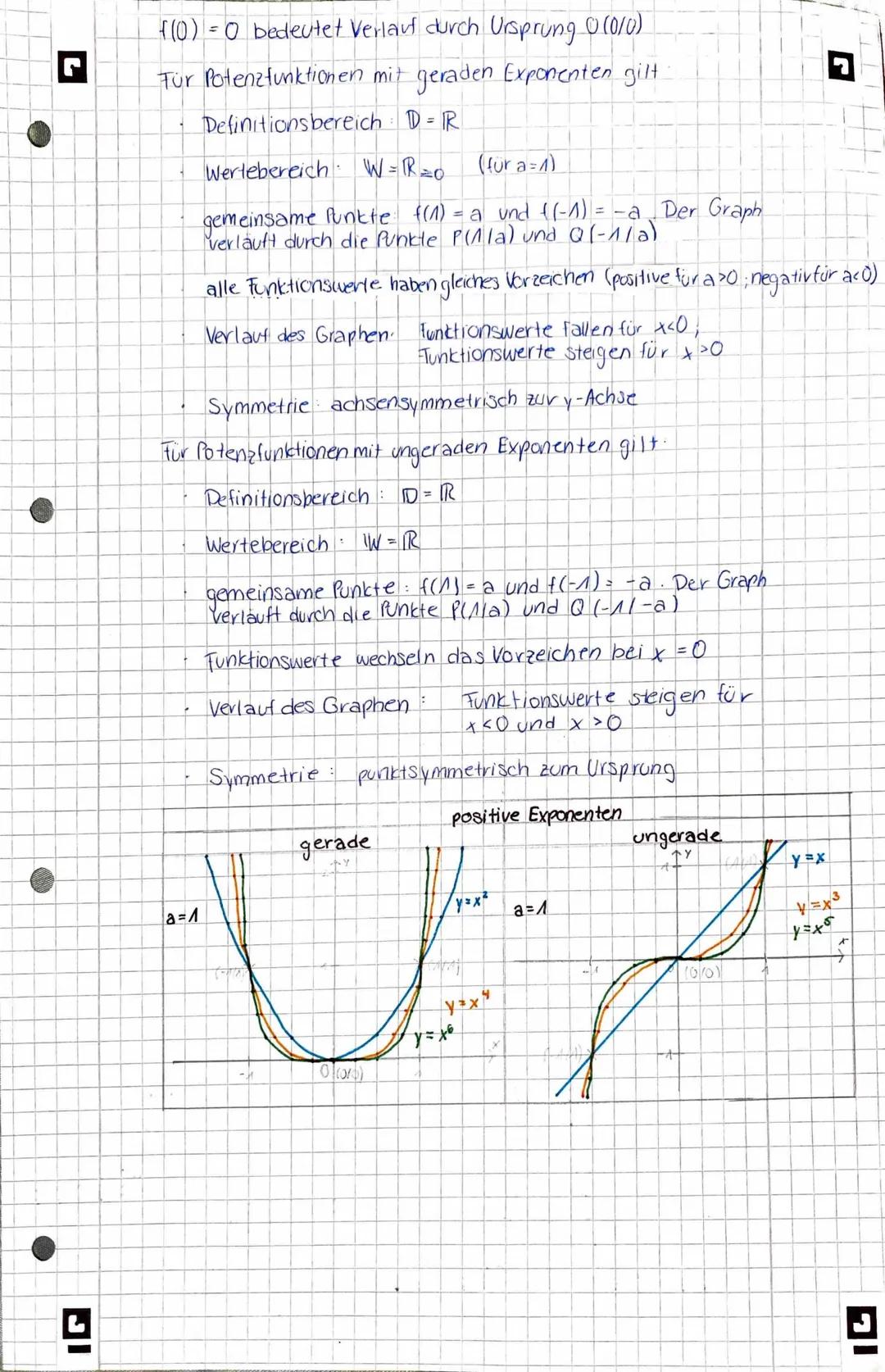
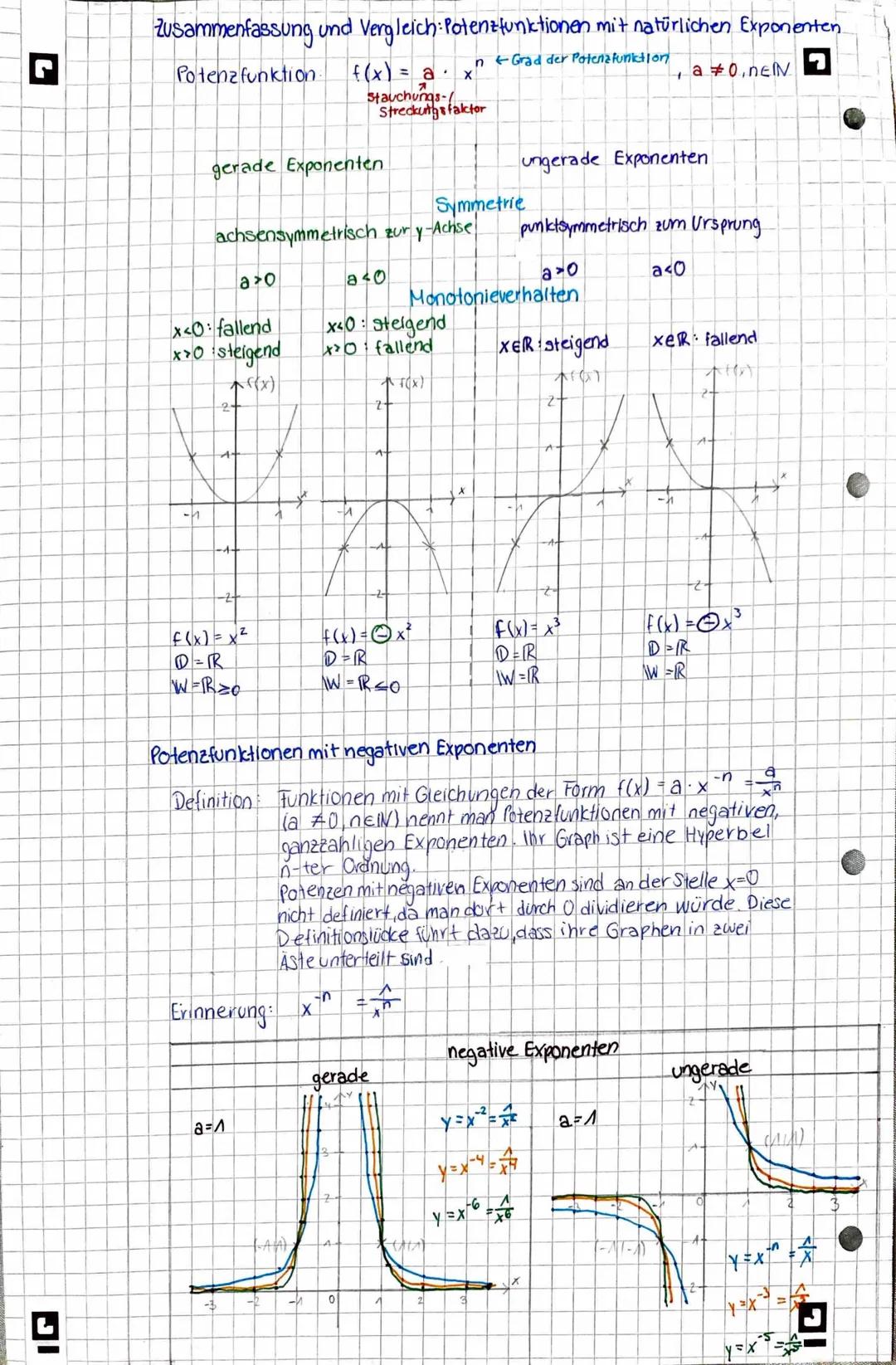
Potenzfunktionen f(x) = a·xⁿ verhalten sich je nach Exponent völlig unterschiedlich. Gerade Exponenten (2, 4, 6...) schaffen achsensymmetrische Graphen zur y-Achse, ungerade Exponenten (1, 3, 5...) punktsymmetrische zum Ursprung.
Bei geraden Exponenten sind alle Funktionswerte positiv (für a > 0), bei ungeraden wechselt das Vorzeichen. Der Streckfaktor a bestimmt: |a| > 1 streckt, |a| < 1 staucht, a < 0 spiegelt an der x-Achse.
Alle Potenzfunktionen laufen durch den Ursprung (0|0) und die charakteristischen Punkte (1|a) und −1∣±a. Das Monotonieverhalten hängt vom Exponenten ab.
Visualisierungstipp: Skizziere immer die Grundform zuerst, dann überlege dir die Transformationen!