Sigma-Regeln - Intervalle um den Erwartungswert
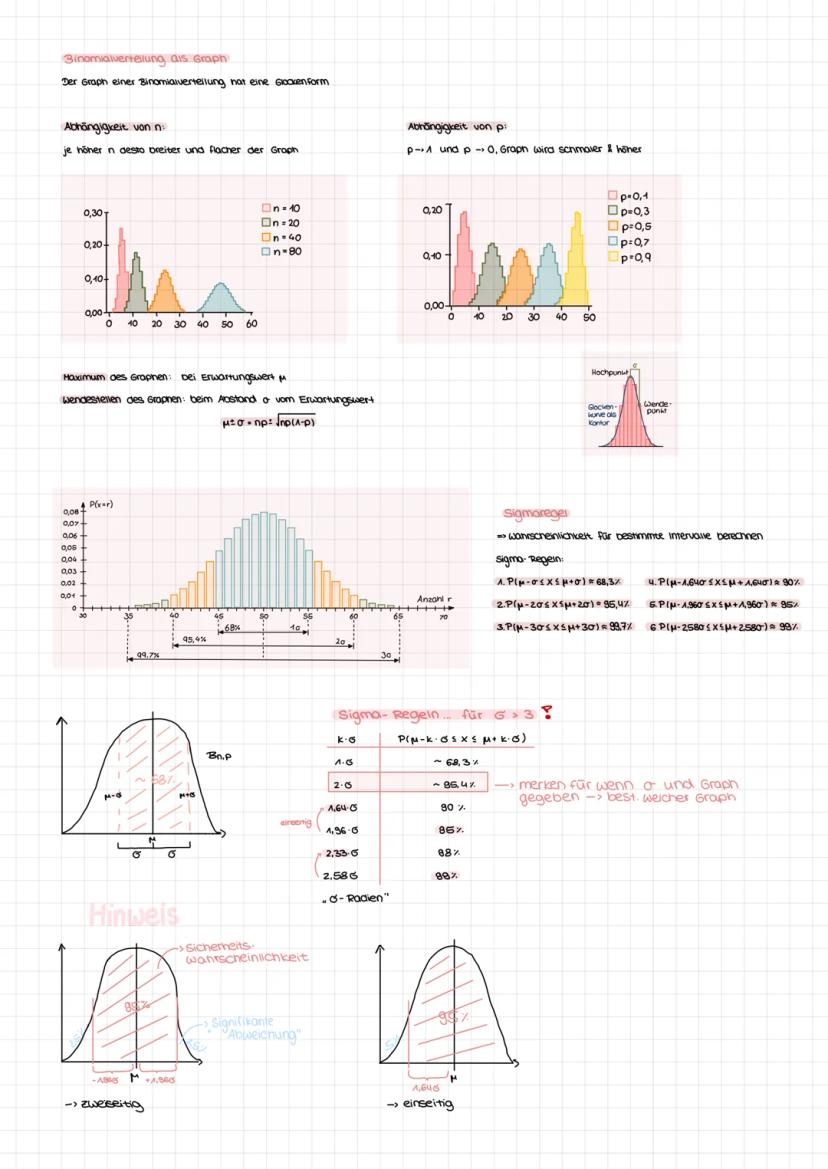
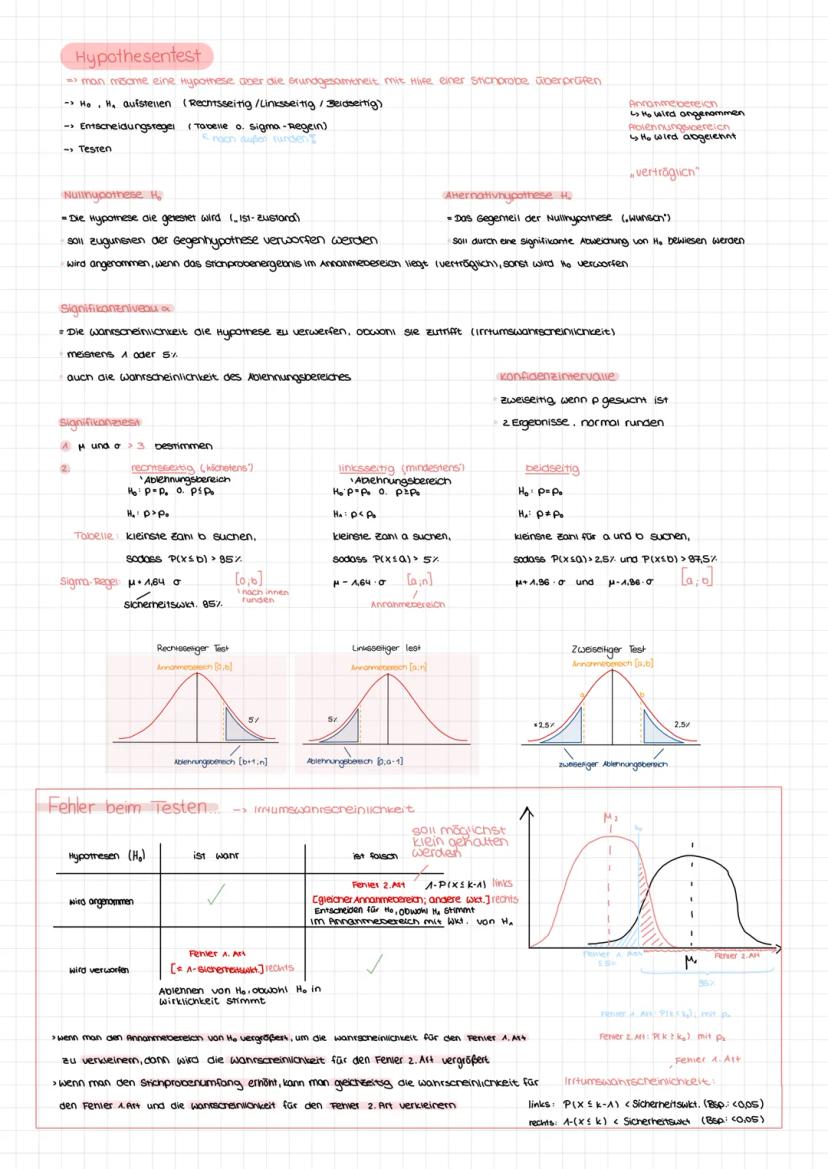
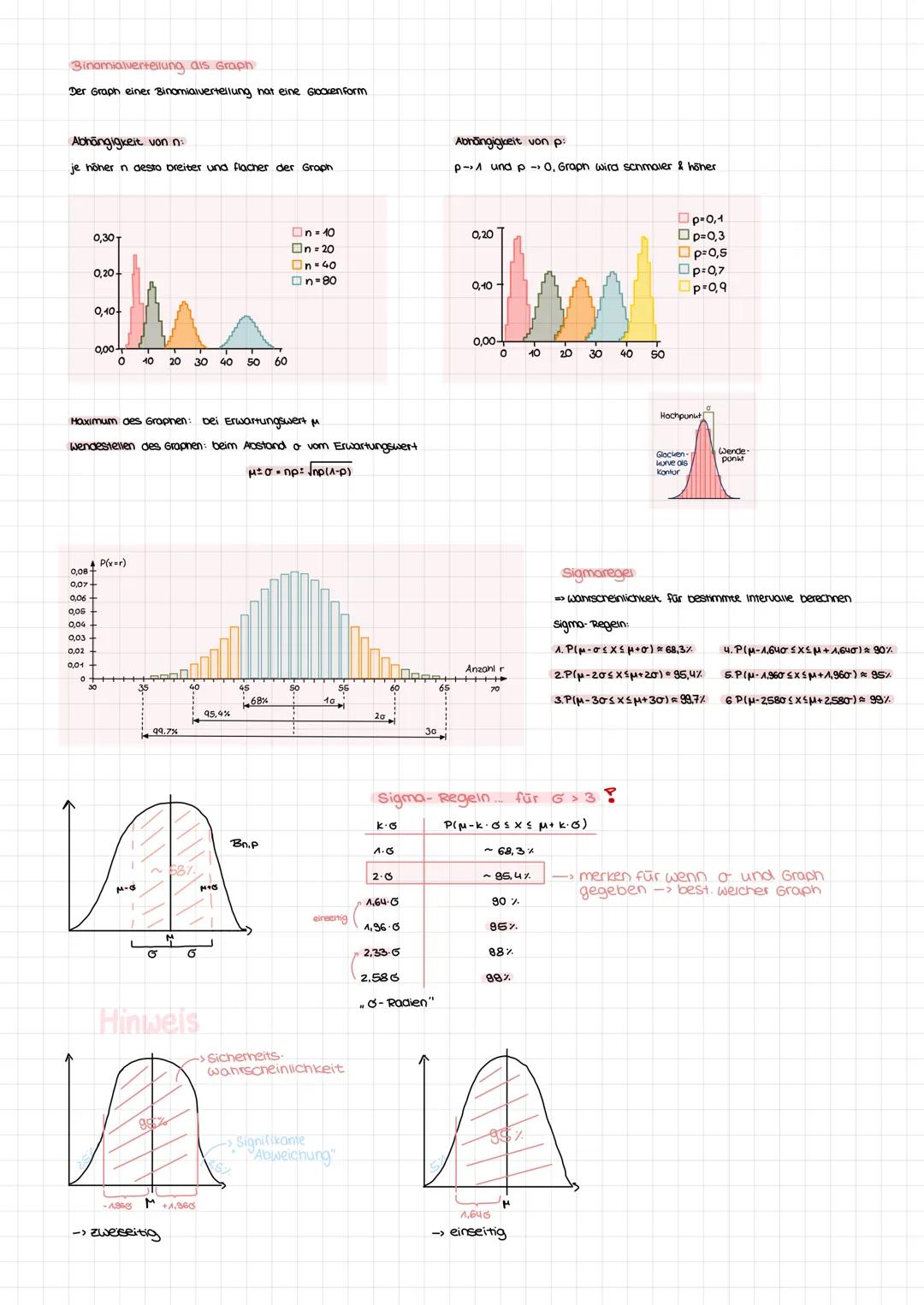
Die Binomialverteilung hat eine charakteristische Glockenform. Der Hochpunkt liegt beim Erwartungswert μ, die Wendepunkte bei μ ± σ. Je größer n, desto breiter und flacher wird der Graph.
Die Sigma-Regeln geben dir wichtige Faustregeln: Etwa 68% aller Werte liegen im 1σ-Intervall um μ, 95% im 2σ-Intervall und 99,7% im 3σ-Intervall. Diese Regeln gelten nur bei σ ≥ 3.
Für Konfidenzintervalle merkst du dir: 90% entspricht ±1,64σ, 95% entspricht ±1,96σ, 99% entspricht ±2,58σ. Diese Werte brauchst du später für Hypothesentests.
💡 Visualisierung: Stell dir die Glocke vor - die meisten Werte sammeln sich in der Mitte, wenige an den Rändern!