Grundlagen der Kinematik

Bewegungen sind Ortsveränderungen von Körpern über einen bestimmten Zeitraum und werden immer relativ zu einem Bezugssystem beschrieben. Beim Betrachten von Bewegungen unterscheiden wir hauptsächlich zwischen gleichförmigen (konstante Geschwindigkeit) und gleichmäßig beschleunigten Bewegungen.

Um zu bestimmen, wie schnell sich ein Körper bewegt, nutzen wir die Durchschnittsgeschwindigkeit. Sie wird berechnet, indem wir die zurückgelegte Strecke Δs durch die dafür benötigte Zeit Δt teilen: v = Δs/Δt. Mathematisch entspricht dies der Steigung einer Sekante im s-t-Diagramm.

Die Momentangeschwindigkeit gibt an, wie schnell ein Körper zu einem bestimmten Zeitpunkt ist. Sie lässt sich als Grenzwert der Durchschnittsgeschwindigkeit für ein unendlich kleines Zeitintervall (Δt→0) bestimmen. In der mathematischen Sprache entspricht dies der ersten Ableitung der Weg-Zeit-Funktion: v = s'(t).

💡 Ein wichtiger Zusammenhang: Der Flächeninhalt unterhalb eines t-v-Graphen entspricht immer dem zurückgelegten Weg – unabhängig davon, ob der Graph gerade oder gekrümmt ist.

Bewegungsarten und ihre Gleichungen

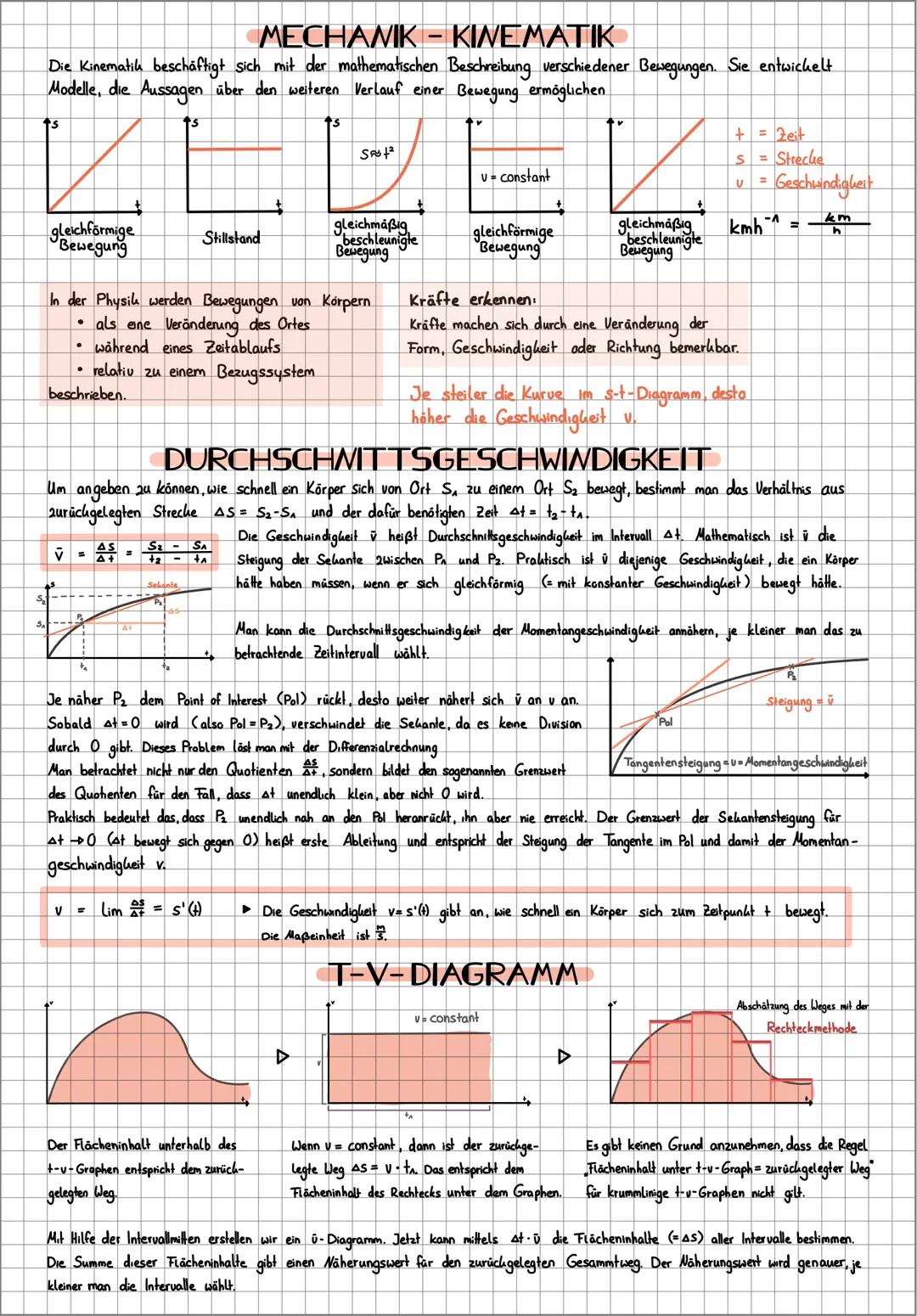
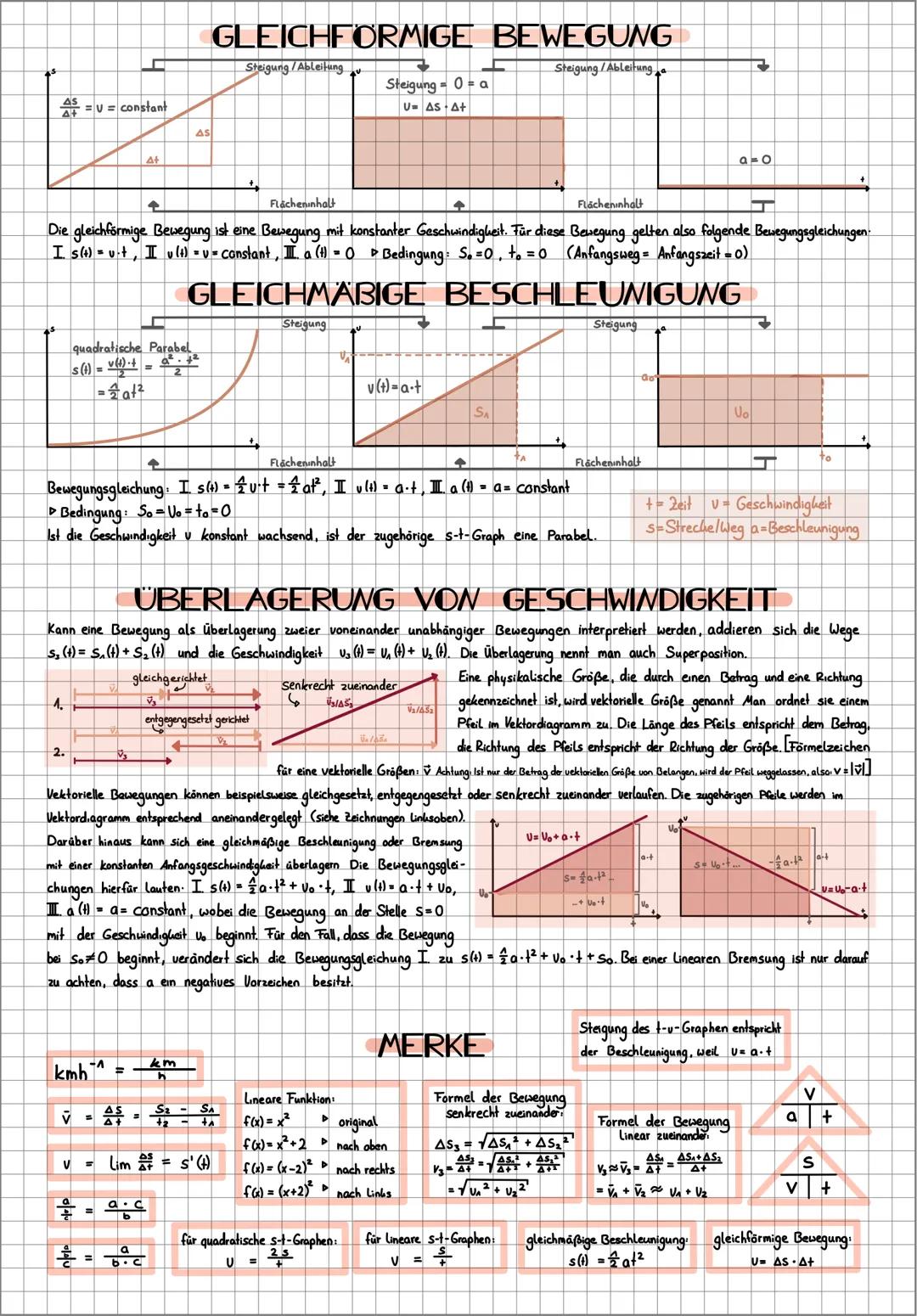
Bei der gleichförmigen Bewegung ist die Geschwindigkeit konstant $v = konstant$ und die Beschleunigung ist null $a = 0$. Der s-t-Graph ist eine Gerade, deren Steigung der Geschwindigkeit entspricht. Die Bewegungsgleichung lautet s(t) = v·t (wenn der Anfangsweg null ist).

Die gleichmäßig beschleunigte Bewegung zeichnet sich durch eine konstante Beschleunigung aus. Hier ist der s-t-Graph eine Parabel und der v-t-Graph eine Gerade. Die wichtigsten Gleichungen sind: s(t) = ½at² und v(t) = a·t (wenn Anfangsweg und Anfangsgeschwindigkeit null sind).

Bei Überlagerung von Bewegungen addieren sich die Wege und Geschwindigkeiten. Dieses Prinzip nennt man Superposition. Je nach Richtung der Bewegungen unterscheiden wir zwischen gleichgerichteten, entgegengesetzten und senkrecht zueinander verlaufenden Bewegungen.

🔑 Merke: Die Steigung im t-v-Graphen entspricht der Beschleunigung. Bei senkrecht zueinander verlaufenden Bewegungen berechnet sich der Gesamtweg nach dem Satz des Pythagoras: Δs₃ = √$Δs₁² + Δs₂²$.

Wenn eine gleichmäßige Beschleunigung mit einer Anfangsgeschwindigkeit v₀ kombiniert wird, erweitern sich die Bewegungsgleichungen zu: s(t) = ½at² + v₀t und v(t) = at + v₀. Auch eine lineare Bremsung lässt sich mit diesen Gleichungen beschreiben, indem man für a einen negativen Wert einsetzt.