Natürliche Exponentialfunktionen

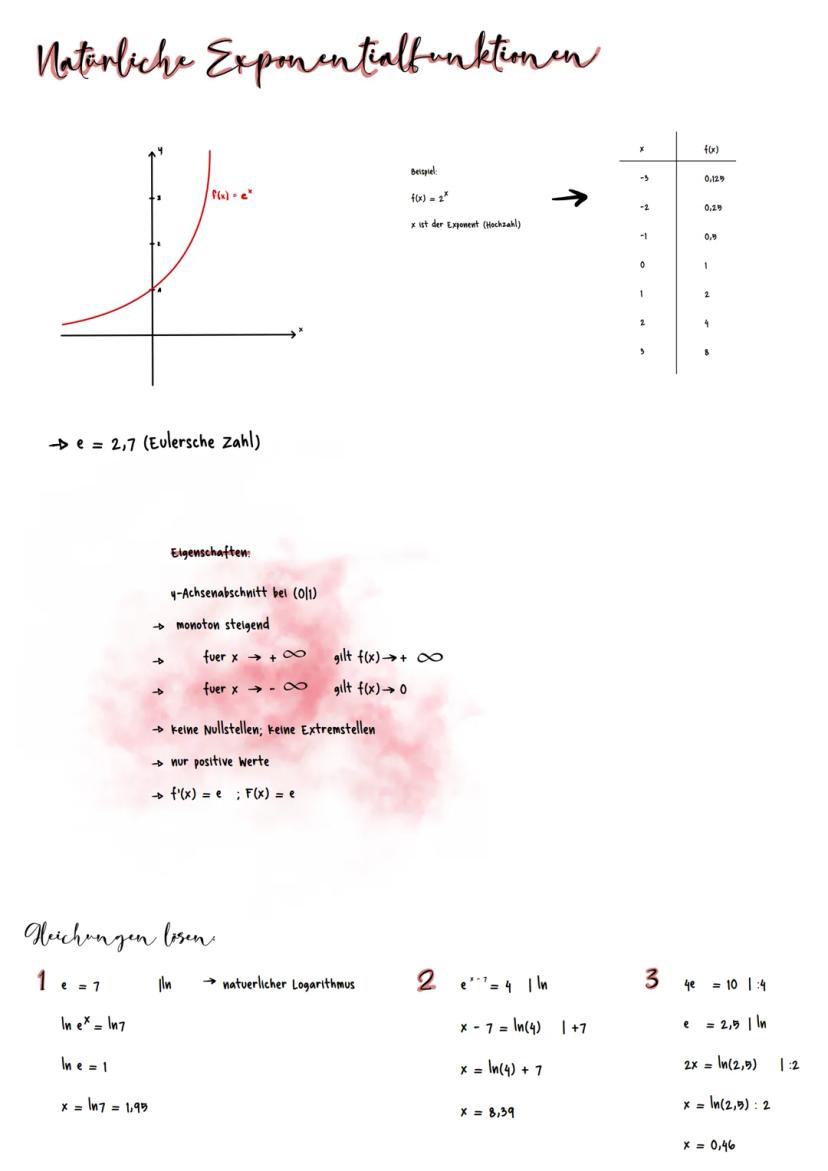
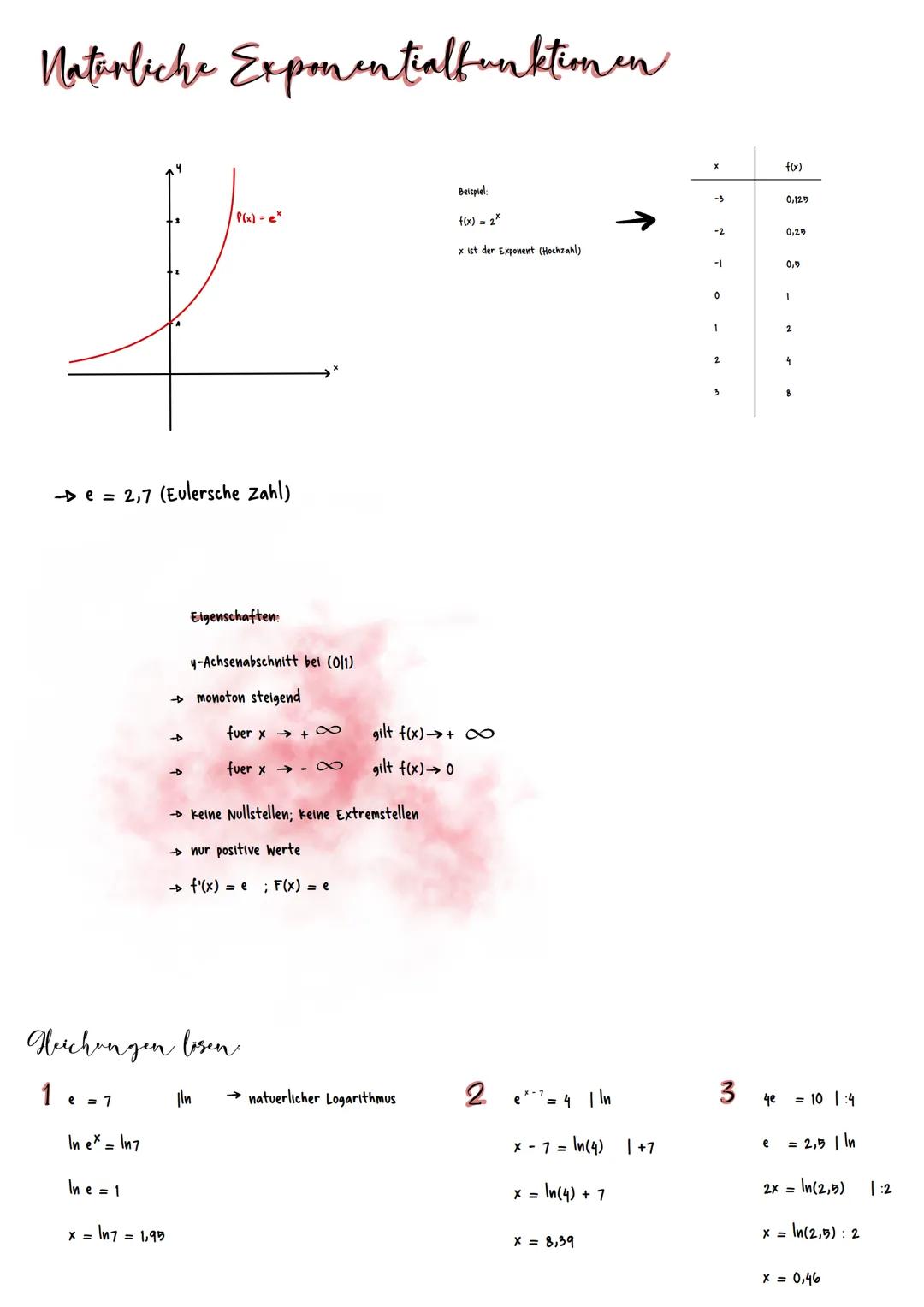
Die Funktion f$x$ = e^x ist eine besondere Exponentialfunktion mit der Eulerschen Zahl e ≈ 2,7 als Basis. Sie hat wichtige Eigenschaften: Sie schneidet die y-Achse bei (0|1), ist monoton steigend und nimmt nur positive Werte an. Für x → +∞ geht f$x$ → +∞, und für x → -∞ geht f$x$ → 0.

Das Besondere an dieser Funktion ist, dass ihre Ableitungsfunktion wieder sie selbst ist: f'$x$ = e^x. Dies macht sie in der Differentialrechnung besonders wertvoll.

Bei Exponentialgleichungen mit e nutzen wir den natürlichen Logarithmus (ln) als Gegenstück. Zum Beispiel: Bei e^x = 7 wenden wir auf beiden Seiten ln an und erhalten x = ln(7) ≈ 1,99. Bei komplexeren Gleichungen wie e^$x-7$ = 4 lösen wir schrittweise: Erst ln$e^(x-7)$ = ln(4), dann x-7 = ln(4) und schließlich x = ln(4) + 7 ≈ 8,39.

Merke dir: Die e-Funktion ist die einzige Funktion, die mit ihrer eigenen Ableitung identisch ist. Diese Eigenschaft macht sie für viele Anwendungen in Naturwissenschaften und Wirtschaft so wichtig!

Ableitungen und Tangenten von e-Funktionen

Bei zusammengesetzten Funktionen mit e^x wendest du die normalen Ableitungsregeln an. Beispielsweise wird f$x$ = 2e^x + 3x + 7 zu f'$x$ = 2e^x + 3 und f''$x$ = 2e^x. Der Term mit e^x bleibt nach der Ableitung erhalten, während konstante Terme verschwinden.

Die Tangentengleichung t$x$ = mx + n an eine Funktion lässt sich einfach bestimmen. Du brauchst die Steigung m $= f'(x₀)$ und einen Punkt (x₀|f(x₀)). Bei f$x$ = e^x und x₀ = 0 gilt: f'(0) = e^0 = 1 und f(0) = 1. Daraus folgt n = 1 und somit t$x$ = x + 1.

Beim Lösen von e-Funktionsgleichungen ist der natürliche Logarithmus dein wichtigstes Werkzeug. Isoliere zunächst den Term mit e und wende dann ln an. Bei e^(x²) + 1 = 7 subtrahierst du 1, erhältst e^(x²) = 6, dann x² = ln(6) und schließlich x = ±√ln(6) ≈ ±0,97.

Prüfungstipp: Bei Gleichungen mit e-Funktionen ist der Lösungsweg fast immer: Isolieren der e-Funktion → Anwendung des natürlichen Logarithmus → Auflösen nach der Variablen.

Kettenregel und Produktregel

Bei komplexeren e-Funktionen brauchst du spezielle Ableitungsregeln. Es gibt drei typische Fälle:

1. Verkettung: Bei f$x$ = e^(7x) ist die äußere Funktion e^x und die innere 7x. Nach der Kettenregel ist f'$x$ = e^(7x) · 7 = 7e^(7x). Die Ableitung der inneren Funktion (hier 7) wird mit der äußeren Funktion, angewendet auf die innere $hier e^(7x)$, multipliziert.

2. Produktregel: Bei f$x$ = 2x · e^x multiplizierst du zwei Funktionen. Nach der Formel (u·v)' = u'·v + u·v' erhältst du f'$x$ = 2·e^x + 2x·e^x = e^x$2 + 2x$. Hier ist u$x$ = 2x und v$x$ = e^x.

3. Kombination: Bei f$x$ = $x+2$·e^(3x) wendest du beide Regeln an. Mit u$x$ = x+2 und v$x$ = e^(3x) erhältst du f'$x$ = 1·e^(3x) + $x+2$·3e^(3x) = e^(3x)$1 + 3(x+2)$ = e^(3x)$3x + 7$.

Übungstipp: Identifiziere immer zuerst, ob es sich um Verkettung, Produkt oder beides handelt, bevor du mit dem Ableiten beginnst. Das spart Zeit und vermeidet Fehler!