Potenzfunktionen mit natürlichen Exponenten

Potenzfunktionen sind Funktionen mit der Gleichung y = x^n, wobei n eine natürliche Zahl ist. Sie sind super wichtig, weil sie viele reale Situationen beschreiben können.

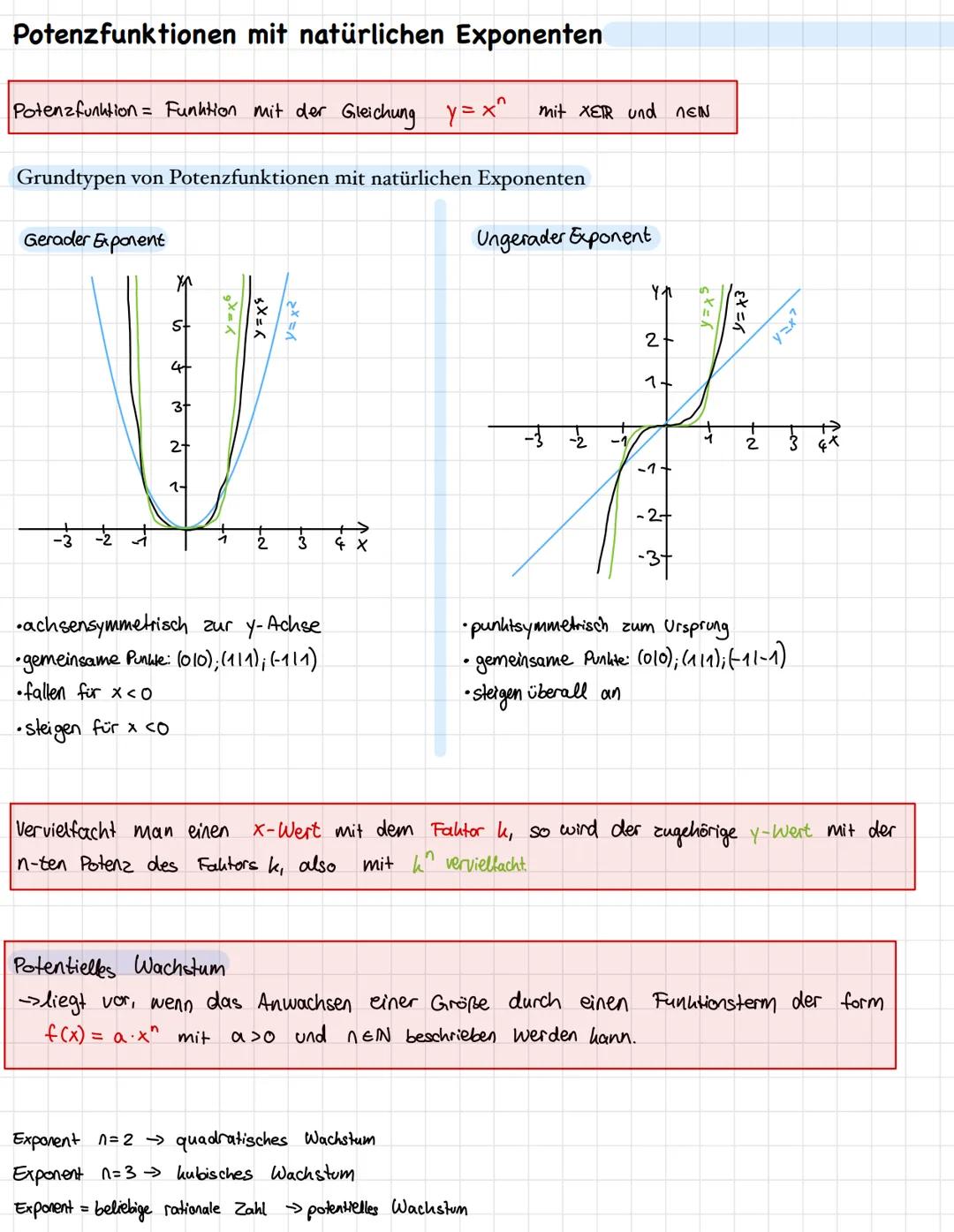
Die wichtigste Unterscheidung liegt zwischen geraden und ungeraden Exponenten. Bei geraden Exponenten (wie x², x⁴) entstehen achsensymmetrische Graphen zur y-Achse - sie sehen aus wie U-förmige Parabeln. Bei ungeraden Exponenten (wie x¹, x³) sind die Graphen punktsymmetrisch zum Ursprung.

Alle Potenzfunktionen haben drei gemeinsame Punkte: (0|0), (1|1) und bei geraden Exponenten zusätzlich (-1|1), bei ungeraden (-1|-1). Das ist ein echter Lifehack für Klassenarbeiten!

Merktipp: Gerade Exponenten = achsensymmetrisch wie ein "U", ungerade Exponenten = punktsymmetrisch wie ein "S"

Ein cooles Feature: Wenn du einen x-Wert mit dem Faktor k multiplizierst, wird der y-Wert mit k^n multipliziert. Das nennt man potentielles Wachstum und kommt in der Realität ständig vor - beim quadratischen Wachstum $n=2$ für Flächen oder beim kubischen Wachstum $n=3$ für Volumen.