Hilfsmittelfreier Teil - Streifenmethode und Grundlagen

Die Streifenmethode ist dein Einstieg in die Integralrechnung und zeigt dir, wie man Flächen näherungsweise berechnet. Bei der Aufgabe mit f(x) = x² + 1 im Intervall [0;2] teilst du die Fläche in 4 gleiche Streifen auf.

Untersumme und Obersumme funktionieren so: Bei der Untersumme nimmst du den kleinsten Funktionswert jedes Streifens, bei der Obersumme den größten. Das gibt dir eine untere und obere Grenze für die tatsächliche Fläche.

Die Flächeninhaltsfunktion A_f(x) ist nichts anderes als die Stammfunktion deiner ursprünglichen Funktion. Damit berechnest du exakte Flächeninhalte zwischen zwei Grenzen - viel präziser als die Streifenmethode.

Merktipp: Je mehr Streifen du verwendest, desto genauer wird deine Näherung!

Stammfunktionen und Grenzwertbetrachtung

Stammfunktionen finden ist wie rückwärts ableiten - du erhöhst den Exponenten um 1 und teilst durch die neue Zahl. Bei f(x) = ⅓x² + 2x wird daraus F(x) = ⅑x³ + x² + C. Das C ist die Integrationskonstante und immer dabei!

Spezialfälle wie e-Funktionen und trigonometrische Funktionen haben ihre eigenen Regeln. Bei f(x) = e^$3x+1$ teilst du durch die innere Ableitung, hier also durch 3.

Die Summenformel-Aufgabe zeigt dir, wie aus der Streifenmethode das echte Integral wird. Du berechnest erst die Produktsumme S_n und lässt dann n gegen unendlich gehen - das ist der Grenzwert.

Eine bestimmte Stammfunktion findest du, wenn ein Punkt gegeben ist. Du bestimmst erst die allgemeine Stammfunktion und setzt dann den Punkt ein, um C zu berechnen.

Praxistipp: Kontrolliere deine Stammfunktionen immer durch Ableiten - so findest du Fehler sofort!

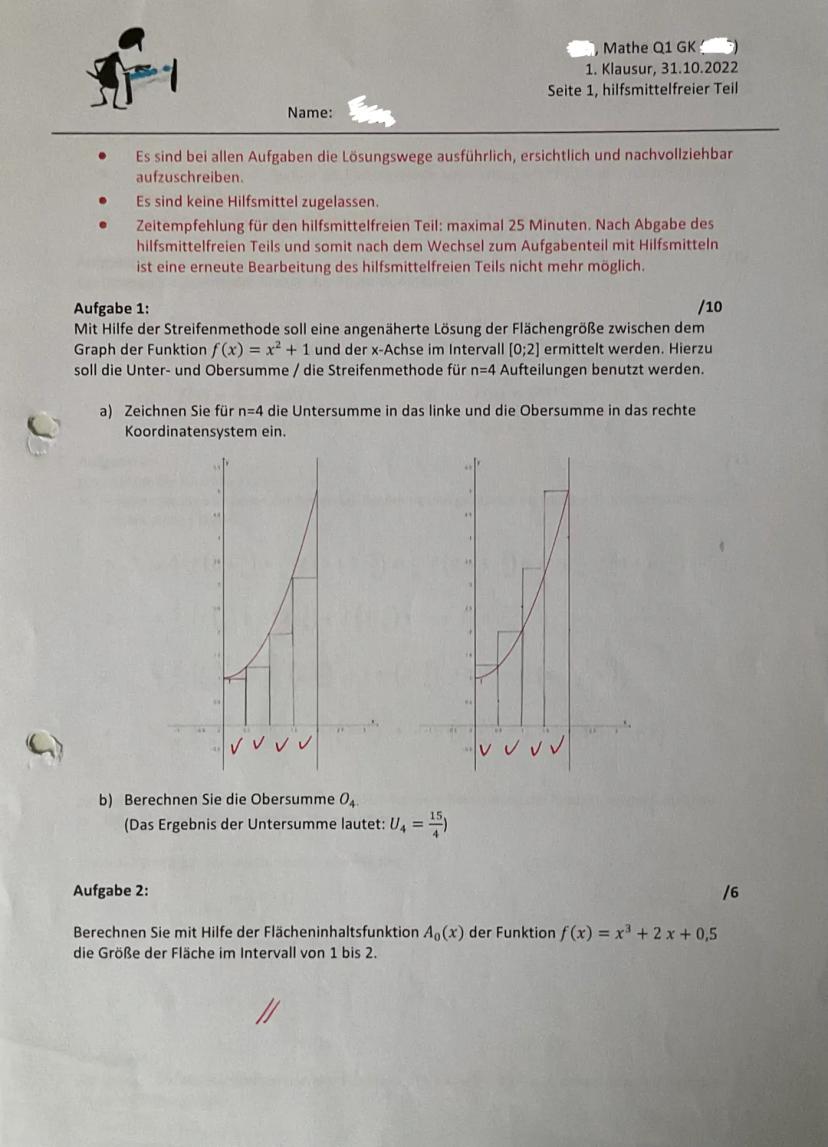
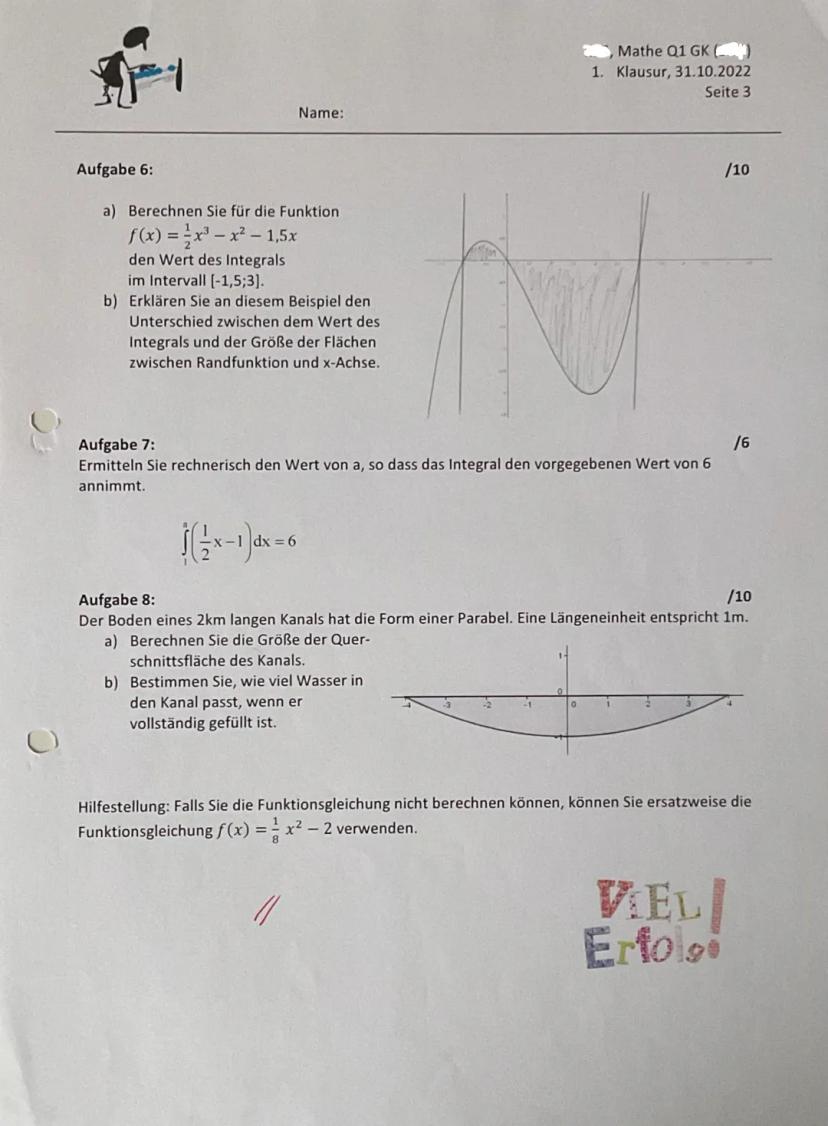
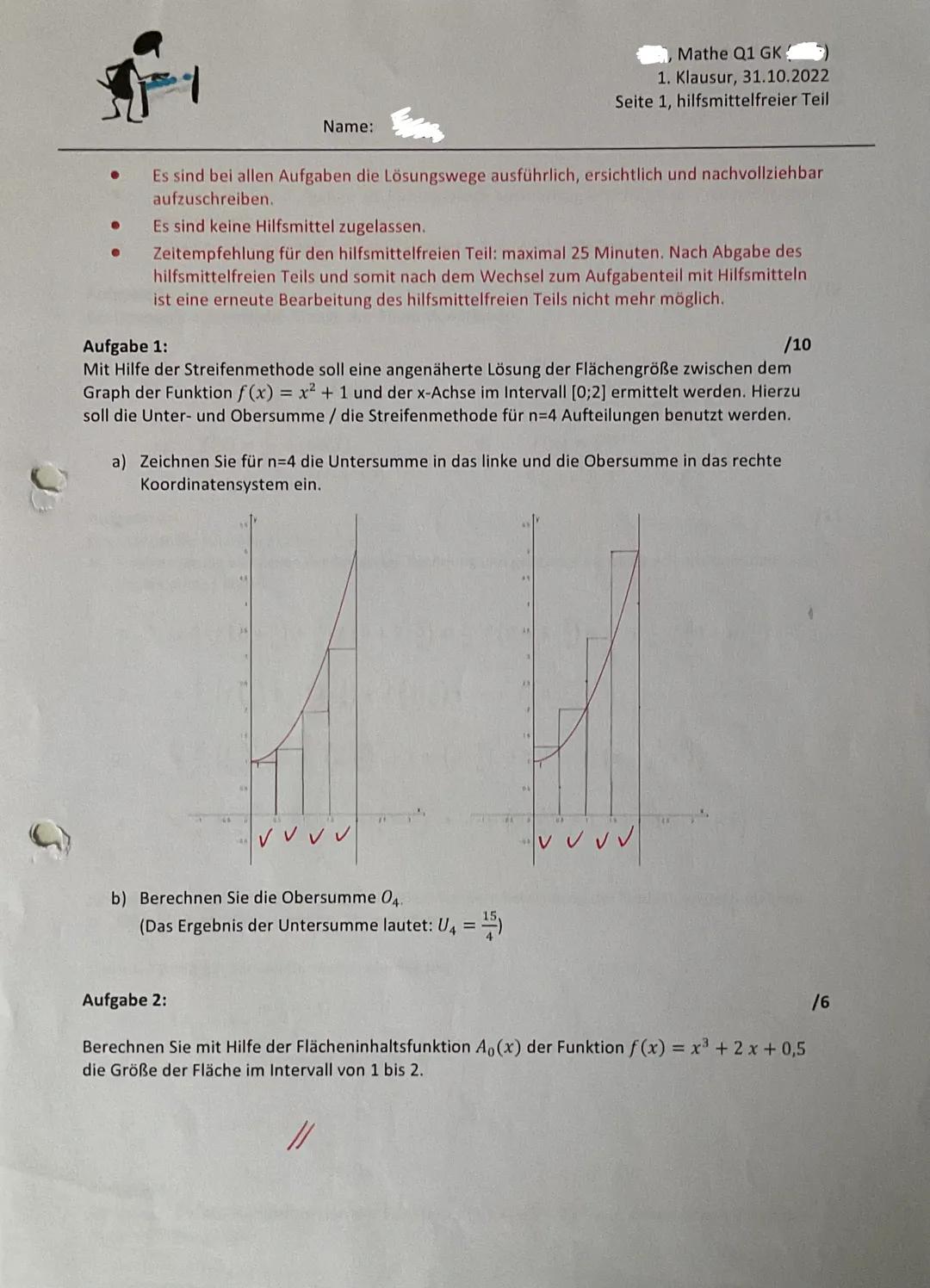
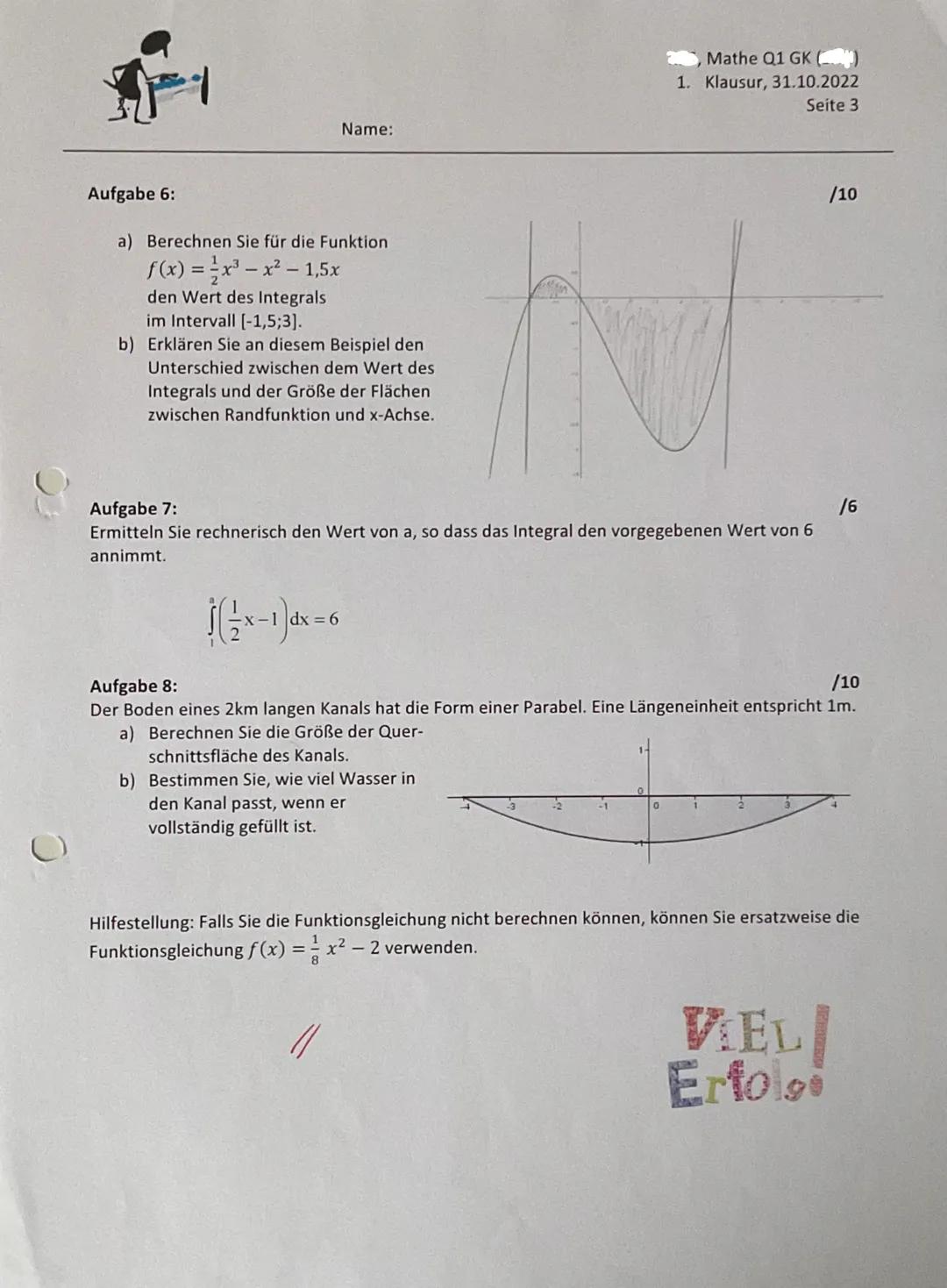
Integrale berechnen und anwenden

Bestimmte Integrale berechnest du mit der Formel $F(b) - F(a)$. Wichtig: Das Ergebnis kann negativ sein, wenn die Funktion unter der x-Achse verläuft - das ist der Unterschied zwischen Integralwert und Flächeninhalt.

Bei Flächenberechnungen musst du aufpassen: Liegt die Funktion teilweise unter der x-Achse, musst du die Beträge der einzelnen Teilflächen addieren, nicht einfach das Integral berechnen.

Integralgleichungen löst du, indem du das Integral ausrechnest und dann nach der unbekannten Grenze auflöst. Bei ∫_{-1}^a $x-1$dx = 6 setzt du die Stammfunktion ein und löst die entstehende Gleichung.

Anwendungsaufgaben wie der Kanal zeigen dir, warum Integrale wichtig sind: Du berechnest erst die Querschnittsfläche mit einem Integral und multiplizierst dann mit der Länge für das Volumen.

Erfolgstrick: Zeichne dir bei Flächenaufgaben immer eine kleine Skizze - so siehst du sofort, wo die Funktion positiv oder negativ ist!