Grundbegriffe der Stochastik

Stell dir vor, du würfelst oder ziehst Kugeln aus einer Urne - das sind typische Zufallsprozesse. Ein Zufallsprozess ist ein Vorgang, der theoretisch unendlich oft wiederholt werden kann und dessen Ausgang ungewiss ist.

Der Ergebnisraum Ω (Omega) umfasst alle möglichen Ausgänge deines Experiments. Beim Würfeln wäre das Ω = {1;2;3;4;5;6}. Ein einzelnes Ergebnis ist dann z.B. die gewürfelte 3.

Ein Ereignis E fasst mehrere mögliche Ergebnisse zusammen - es ist eine Teilmenge des Ergebnisraums. Das Ereignis "gerade Zahl" beim Würfeln hätte die Ergebnismenge E = {2;4;6}. Die Wahrscheinlichkeit eines Ereignisses schreibst du als P(E).

Merktipp: Das Gegenereignis Ē tritt genau dann ein, wenn E nicht eintritt - beim Ereignis "gerade Zahl" wäre das Gegenereignis "ungerade Zahl" mit Ē = {1;3;5}.

Häufigkeiten und Wahrscheinlichkeiten

Die absolute Häufigkeit gibt an, wie oft ein Ereignis bei deinen Versuchen aufgetreten ist - z.B. "22 mal die 6 geworfen". Die relative Häufigkeit setzt das ins Verhältnis zur Gesamtzahl: absolute Häufigkeit geteilt durch Anzahl der Versuche.

Das Gesetz der großen Zahlen besagt: Bei unendlich vielen Wiederholungen nähert sich die relative Häufigkeit einer festen Zahl zwischen 0 und 1 an - das ist die Wahrscheinlichkeit P(E).

Laplace-Experimente sind besonders einfach, weil alle Ergebnisse gleich wahrscheinlich sind (wie beim fairen Würfel). Hier gilt: P(E) = Anzahl günstiger Ergebnisse / Anzahl möglicher Ergebnisse.

Praxistipp: Beim Würfeln ist P("gerade Zahl") = 3/6 = 1/2, da es 3 günstige (2,4,6) von 6 möglichen Ergebnissen gibt.

Rechenregeln und Baumdiagramme

Für Wahrscheinlichkeiten gelten wichtige Rechenregeln: Unmögliche Ereignisse haben P(E) = 0, sichere Ereignisse P(E) = 1. Der Additionssatz lautet: P(E₁ ∪ E₂) = P(E₁) + P(E₂) - P(E₁ ∩ E₂).

Mehrstufige Zufallsversuche stellst du mit Baumdiagrammen dar. Jeder Ast zeigt eine Wahrscheinlichkeit, jeder Pfad ein mögliches Gesamtergebnis. Die Pfadregeln sind dein wichtigstes Werkzeug:

1. Pfadwahrscheinlichkeit = Produkt aller Zweigwahrscheinlichkeiten längs des Pfads
2. Ereigniswahrscheinlichkeit = Summe aller zugehörigen Pfadwahrscheinlichkeiten

Beim Ziehen mit Zurücklegen bleiben die Wahrscheinlichkeiten konstant, beim Ziehen ohne Zurücklegen ändern sie sich nach jedem Zug.

Beispiel: Beim zweifachen Würfeln ist P(1,1) = 1/6 · 1/6 = 1/36 nach der ersten Pfadregel.

Kombinatorik und Lottomodell

Die Produktregel der Kombinatorik hilft dir bei Auswahlproblemen: Bei 10 Hemden, 4 Hosen und 7 Krawatten gibt es 10 · 4 · 7 = 280 verschiedene Kombinationen.

Für das Ziehen aus Urnen gibt es drei wichtige Fälle:

• Mit Zurücklegen + mit Reihenfolge: nᵏ Möglichkeiten
• Ohne Zurücklegen + mit Reihenfolge: nn-1$$n-2...$n-k+1$ Möglichkeiten
• Ohne Zurücklegen + ohne Reihenfolge: (n k) = n!/$k!(n-k)!$ Möglichkeiten

Das Lottomodell verwendet den dritten Fall. Bei "6 aus 49" mit 4 Richtigen gilt: P("4 Richtige") = (6 4)·(43 2)/(49 6).

Merkhilfe: Beim Lotto interessiert nur, welche Zahlen gezogen werden - nicht in welcher Reihenfolge. Deshalb Fall 3!

Bedingte Wahrscheinlichkeit und Unabhängigkeit

Bedingte Wahrscheinlichkeit beschreibt Situationen, wo du bereits Informationen hast. P_B(A) ist die Wahrscheinlichkeit für A, wenn B schon eingetreten ist. Die Formel lautet: P_B(A) = P(A ∩ B)/P(B).

Der Multiplikationssatz P(A ∩ B) = P(B) · P_B(A) und der Satz von der totalen Wahrscheinlichkeit P(A) = P(B) · P_B(A) + P(B̄) · P_B̄(A) helfen bei komplexeren Problemen.

Unabhängige Ereignisse beeinflussen sich nicht gegenseitig. Dann gilt: P_A(B) = P(B) oder äquivalent P(A ∩ B) = P(A) · P(B). In der Vierfeldertafel erkennst du Unabhängigkeit daran, dass P(A ∩ B) = P(A) · P(B) ist.

Wichtig: Bei Unabhängigkeit folgt aus einem unabhängigen "Pärchen" automatisch die Unabhängigkeit aller anderen Kombinationen.

Zufallsgrößen und Erwartungswert

Eine Zufallsgröße X ordnet jedem Ergebnis eines Zufallsversuchs eine reelle Zahl zu - z.B. den Gewinn bei einem Spiel. Die Wahrscheinlichkeitsverteilung zeigt dir, welche Werte X mit welcher Wahrscheinlichkeit annimmt.

Der Erwartungswert μ = E(X) ist der durchschnittliche Wert bei vielen Wiederholungen: μ = x₁ · P$X = x₁$ + x₂ · P$X = x₂$ + ... Er gibt deine langfristige Gewinnerwartung an.

Die Varianz V(X) und Standardabweichung σ(X) = √V(X) messen, wie stark die Werte um den Erwartungswert streuen. Je größer σ, desto unvorhersagbarer sind die Ergebnisse.

Faire Spiele haben E(X) = 0 - auf lange Sicht gewinnst und verlierst du gleich viel.

Praxistipp: Ein Histogramm visualisiert die Wahrscheinlichkeitsverteilung als Säulendiagramm - die Säulenhöhe entspricht der Wahrscheinlichkeit.

Binomialverteilung

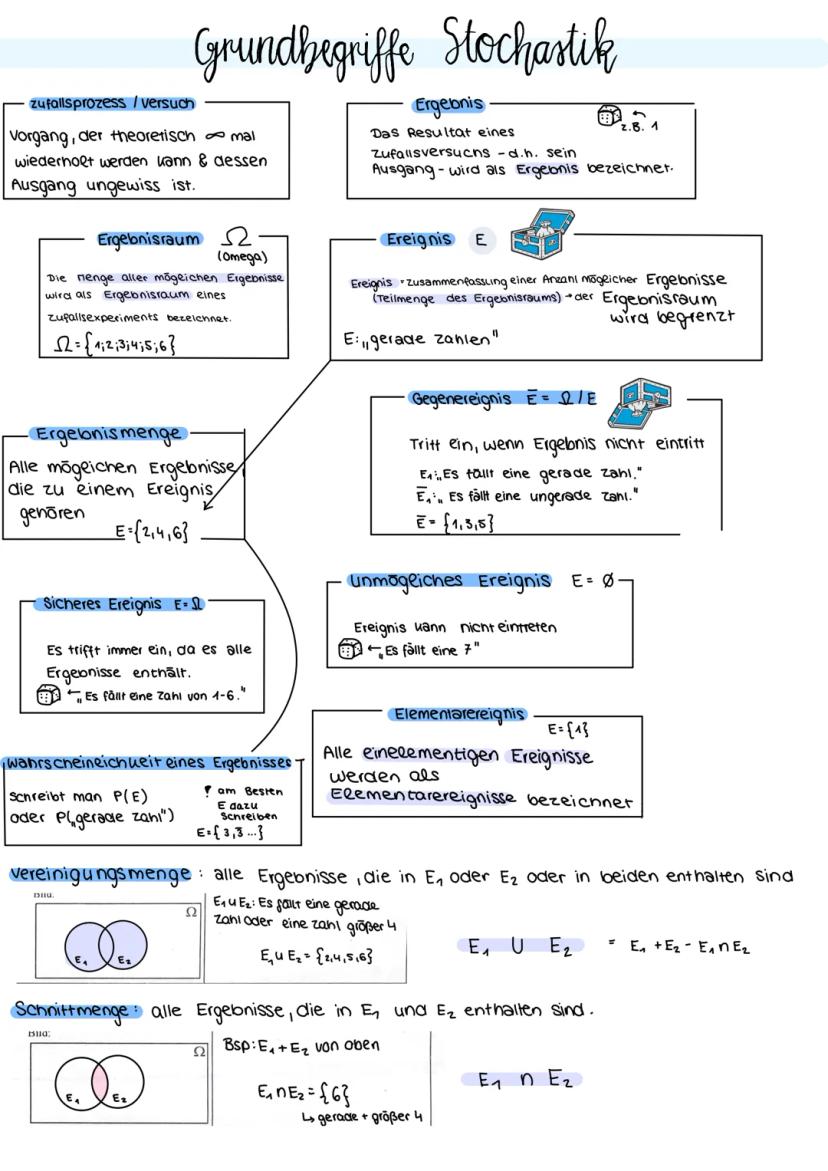
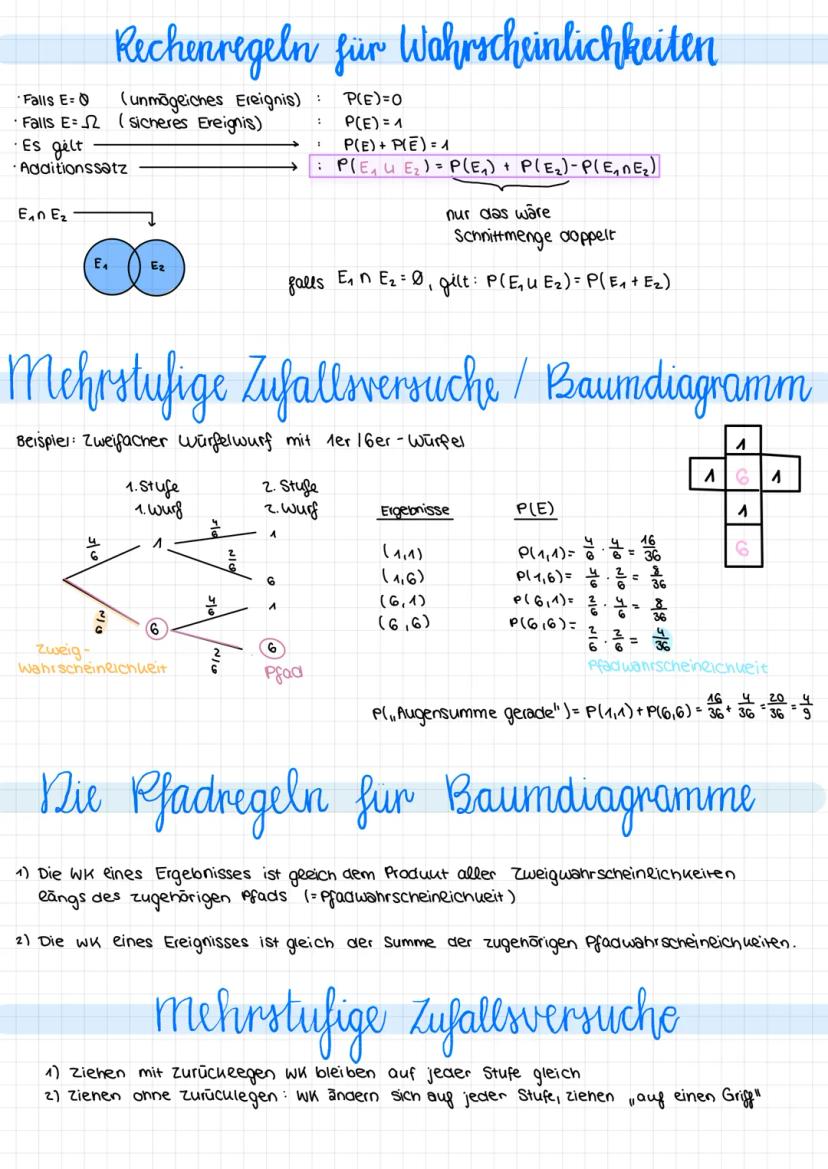
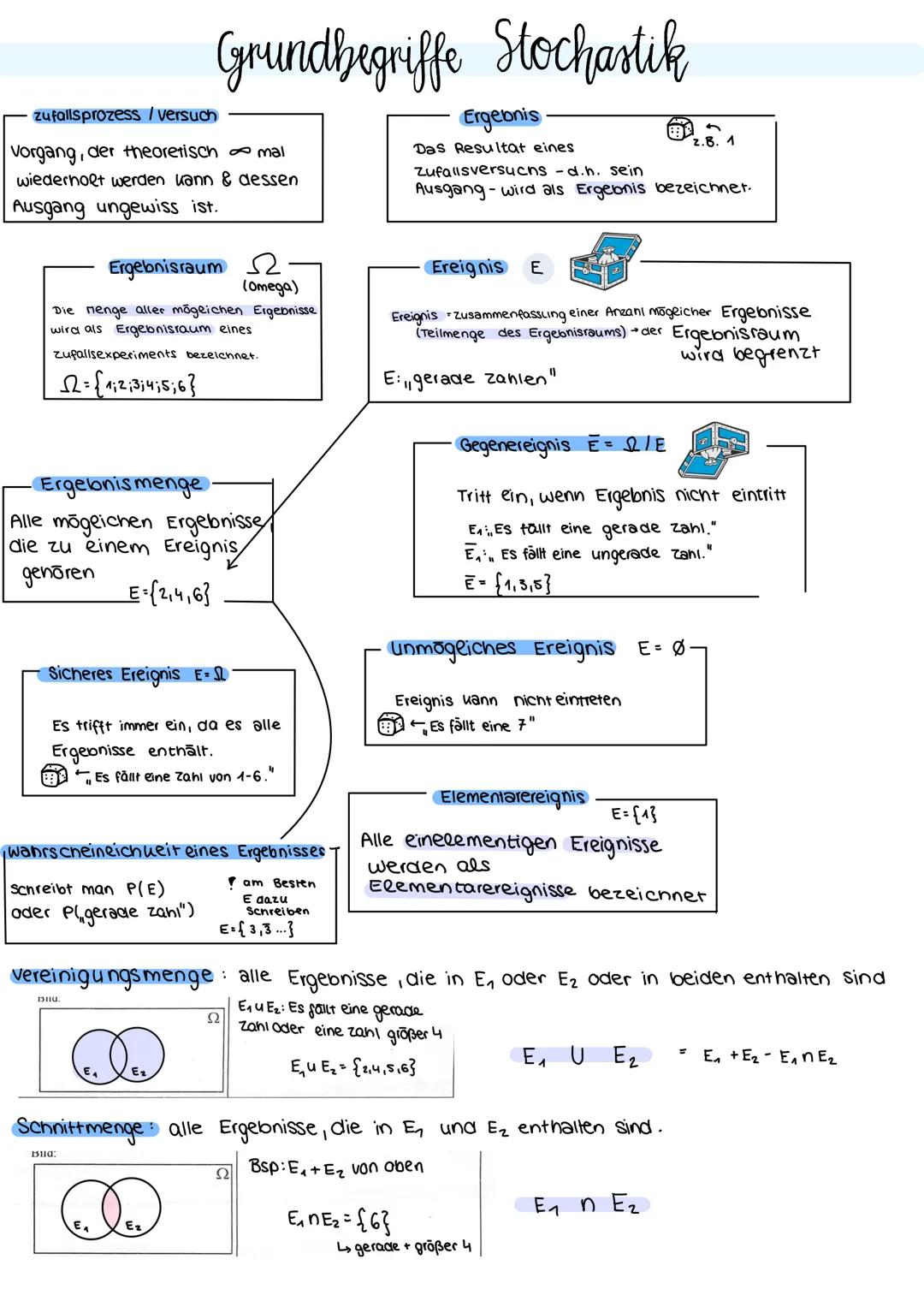
Die Binomialverteilung beschreibt Bernoulli-Ketten - Experimente mit genau zwei Ausgängen (Treffer/Niete), die n-mal mit konstantem p wiederholt werden. Die Zufallsgröße X zählt die Anzahl der Treffer.

Die Wahrscheinlichkeitsformel lautet: P$X = k$ = (n k) · pᵏ · $1-p$ⁿ⁻ᵏ. Diese diskrete Verteilung hat die Parameter n (Anzahl Versuche) und p (Trefferwahrscheinlichkeit).

Im Histogramm siehst du Säulen mit Breite 1 und Höhe P$X = k$. Die Flächensumme aller Säulen ergibt 1, da sich alle Wahrscheinlichkeiten zu 1 addieren.

Typische Beispiele sind Münzwürfe, Qualitätsprüfungen oder Multiple-Choice-Tests. Die Binomialverteilung hilft dir, Fragen wie "Wie wahrscheinlich sind mindestens 3 Treffer bei 10 Versuchen?" zu beantworten.

Merksatz: Bei Bernoulli-Experimenten bleibt p konstant (Ziehen mit Zurücklegen), und es gibt nur zwei mögliche Ausgänge pro Versuch.