Symmetrie von Funktionen

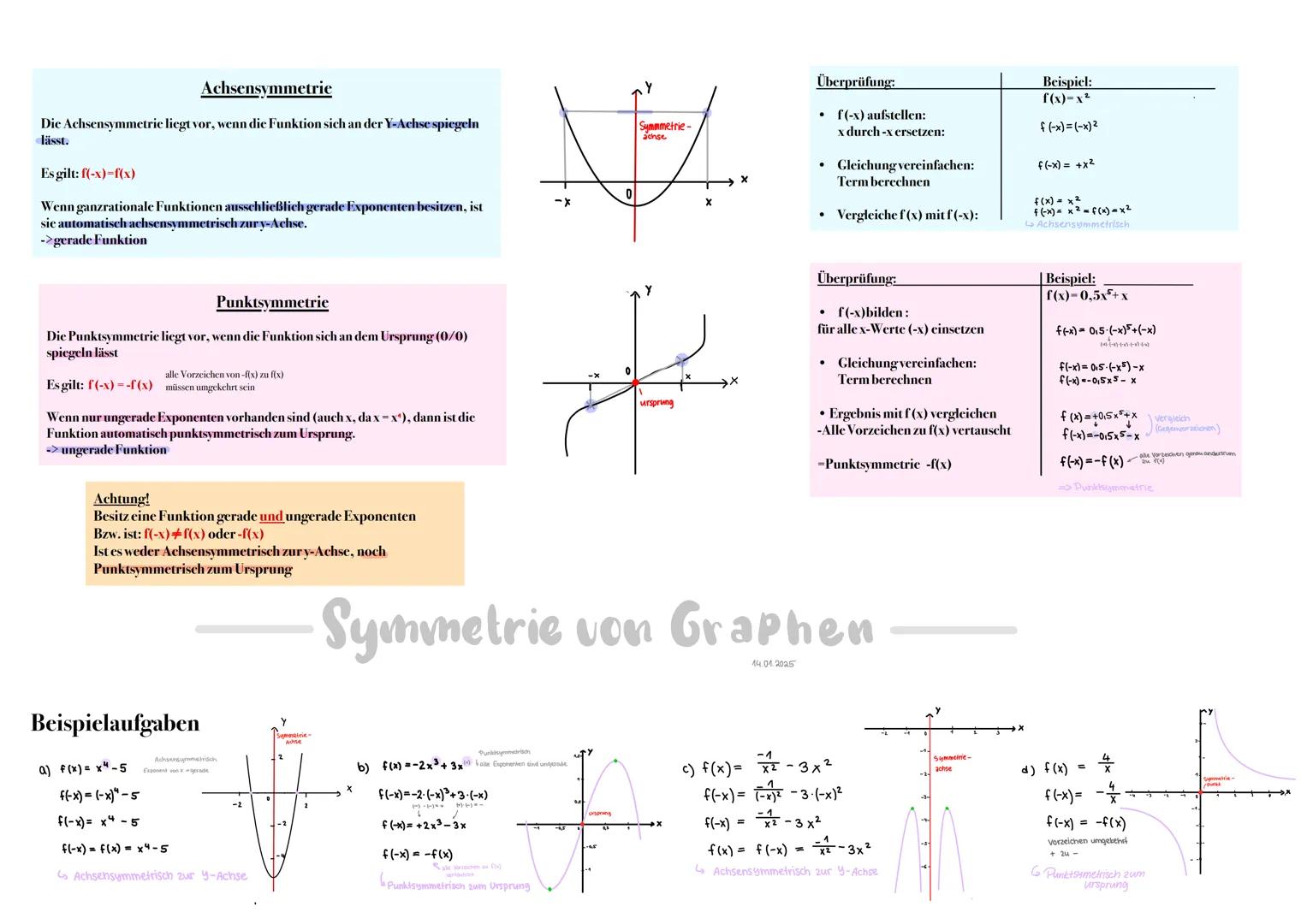
Bei der Achsensymmetrie lässt sich die Funktion an der y-Achse spiegeln. Die wichtige Bedingung dafür ist: f$-x$ = f(x). Du kannst dir das so vorstellen: Wenn du jeden x-Wert mit seinem Gegenwert $-x$ austauschst, erhältst du denselben Funktionswert. Funktionen mit ausschließlich geraden Exponenten (x², x⁴ usw.) sind automatisch achsensymmetrisch zur y-Achse. Man nennt sie auch gerade Funktionen.

Die Punktsymmetrie bedeutet, dass sich die Funktion am Ursprung (0/0) spiegeln lässt. Die Bedingung hier ist: f$-x$ = -f(x). Das heißt, wenn du x durch -x ersetzt, muss sich auch das Vorzeichen des Funktionswertes umkehren. Funktionen mit nur ungeraden Exponenten (x, x³ usw.) sind immer punktsymmetrisch zum Ursprung. Diese werden als ungerade Funktionen bezeichnet.

💡 Merkhilfe: Bei geraden Exponenten erhältst du eine gerade Funktion (achsensymmetrisch), bei ungeraden Exponenten eine ungerade Funktion (punktsymmetrisch).

Wichtig zu wissen: Wenn eine Funktion sowohl gerade als auch ungerade Exponenten enthält $z.B. f(x) = x² + x³$, ist sie weder achsen- noch punktsymmetrisch. In diesem Fall gilt weder f$-x$ = f(x) noch f$-x$ = -f(x).