Trigonometrische Funktionen

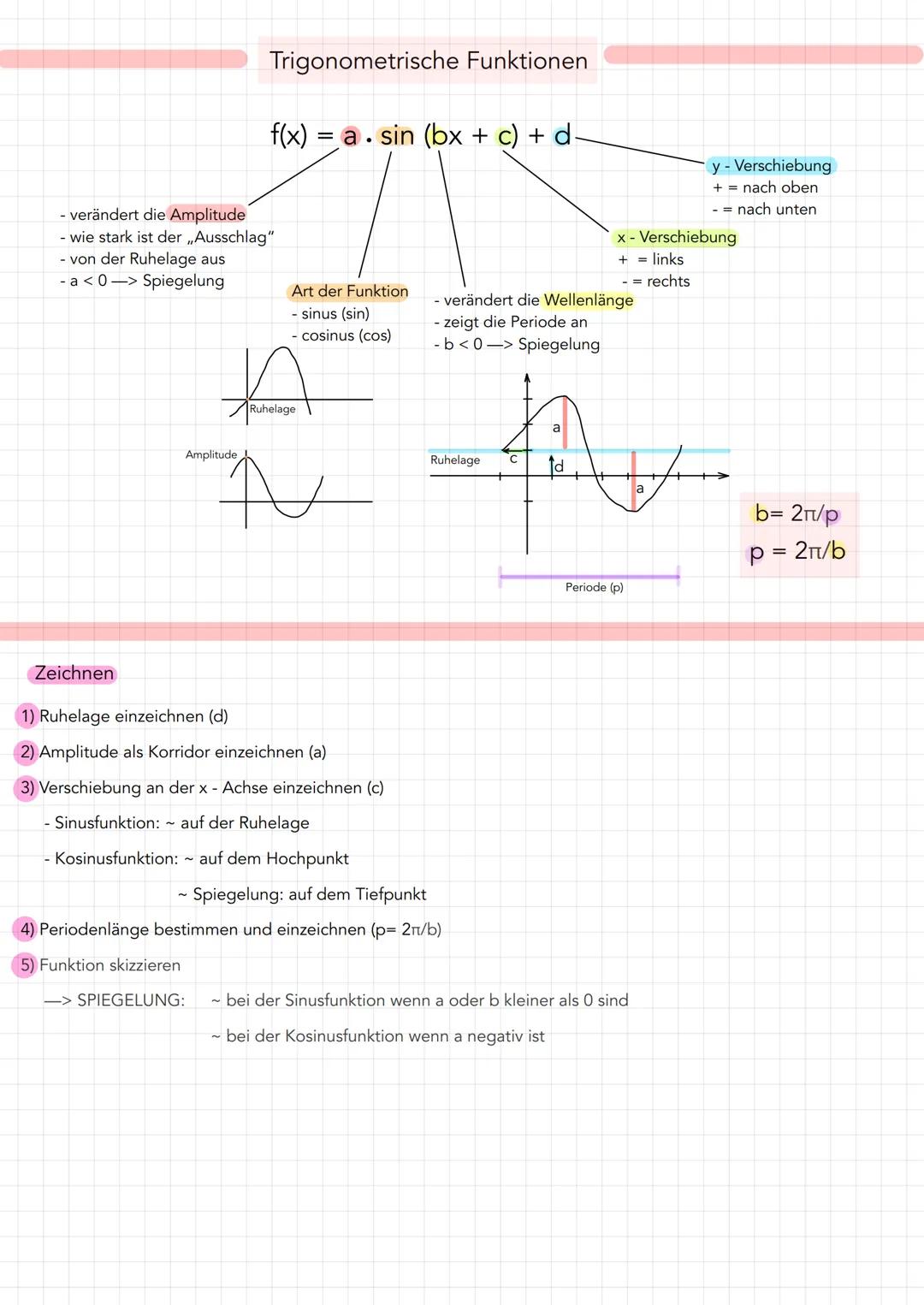
Trigonometrische Funktionen wie Sinus und Kosinus werden durch die Formel $f(x) = a \cdot \sin (bx + c) + d$ oder $f(x) = a \cdot \cos (bx + c) + d$ beschrieben. Jeder Buchstabe hat eine wichtige Bedeutung für das Aussehen der Funktion.

Der Wert a bestimmt die Amplitude – also wie stark der Ausschlag von der Ruhelage ist. Ist a negativ, wird die Funktion an der x-Achse gespiegelt. Der Parameter d verschiebt die gesamte Funktion entlang der y-Achse und bestimmt die Ruhelage. Bei +d geht's nach oben, bei -d nach unten.

Der Faktor b verändert die Wellenlänge und zeigt die Periode an. Es gilt: $b = \frac{2\pi}{p}$ oder umgekehrt $p = \frac{2\pi}{b}$. Bei negativem b wird die Funktion ebenfalls gespiegelt. Der Wert c bewirkt eine Verschiebung entlang der x-Achse – bei +c nach links und bei -c nach rechts.

💡 Merkhilfe: Die Sinusfunktion beginnt immer auf der Ruhelage, während die Kosinusfunktion auf dem Hochpunkt startet. Bei Spiegelungen beginnt der Kosinus auf dem Tiefpunkt!

Zum Zeichnen der Funktionen gehst du schrittweise vor: Zuerst die Ruhelage einzeichnen, dann den Amplitudenkorridor markieren, die x-Verschiebung berücksichtigen, die Periodenlänge bestimmen und schließlich die Kurve skizzieren. Denk an die Spiegelungen: Bei Sinus, wenn a oder b negativ sind; bei Kosinus, wenn a negativ ist.