Funktionsuntersuchungen systematisch durchführen
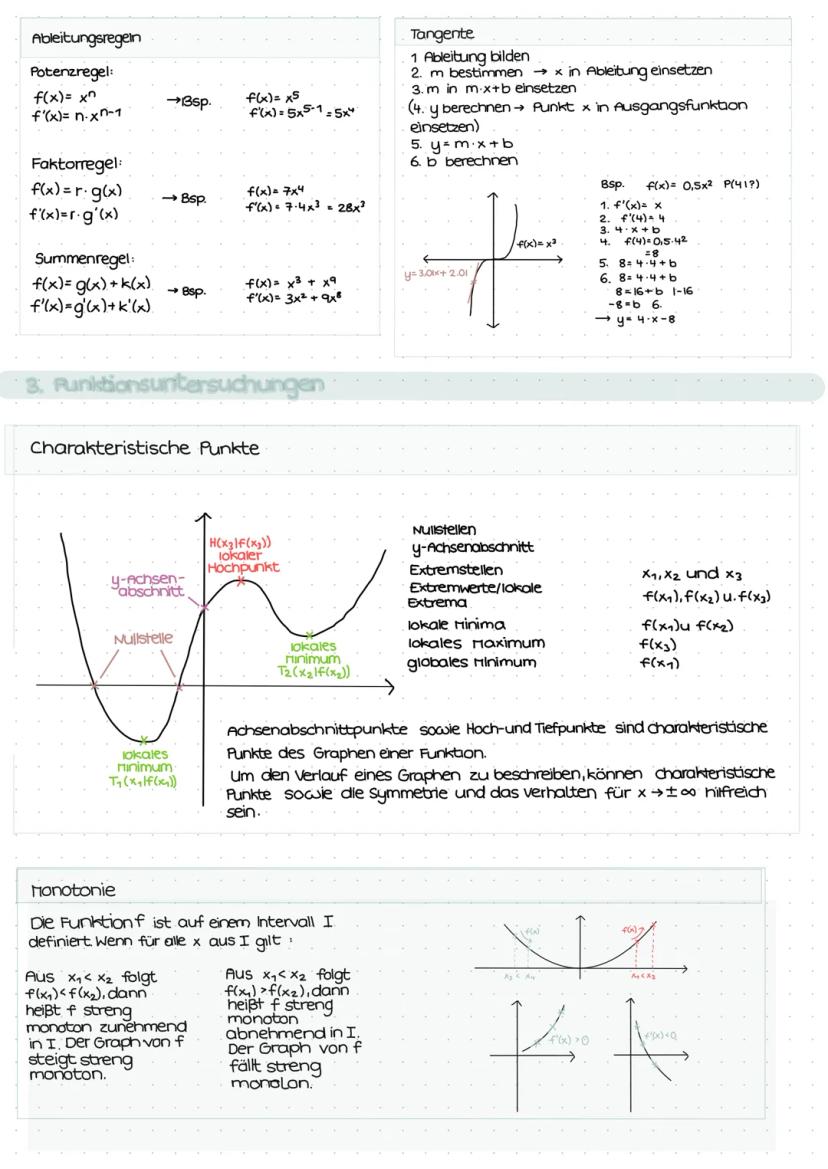
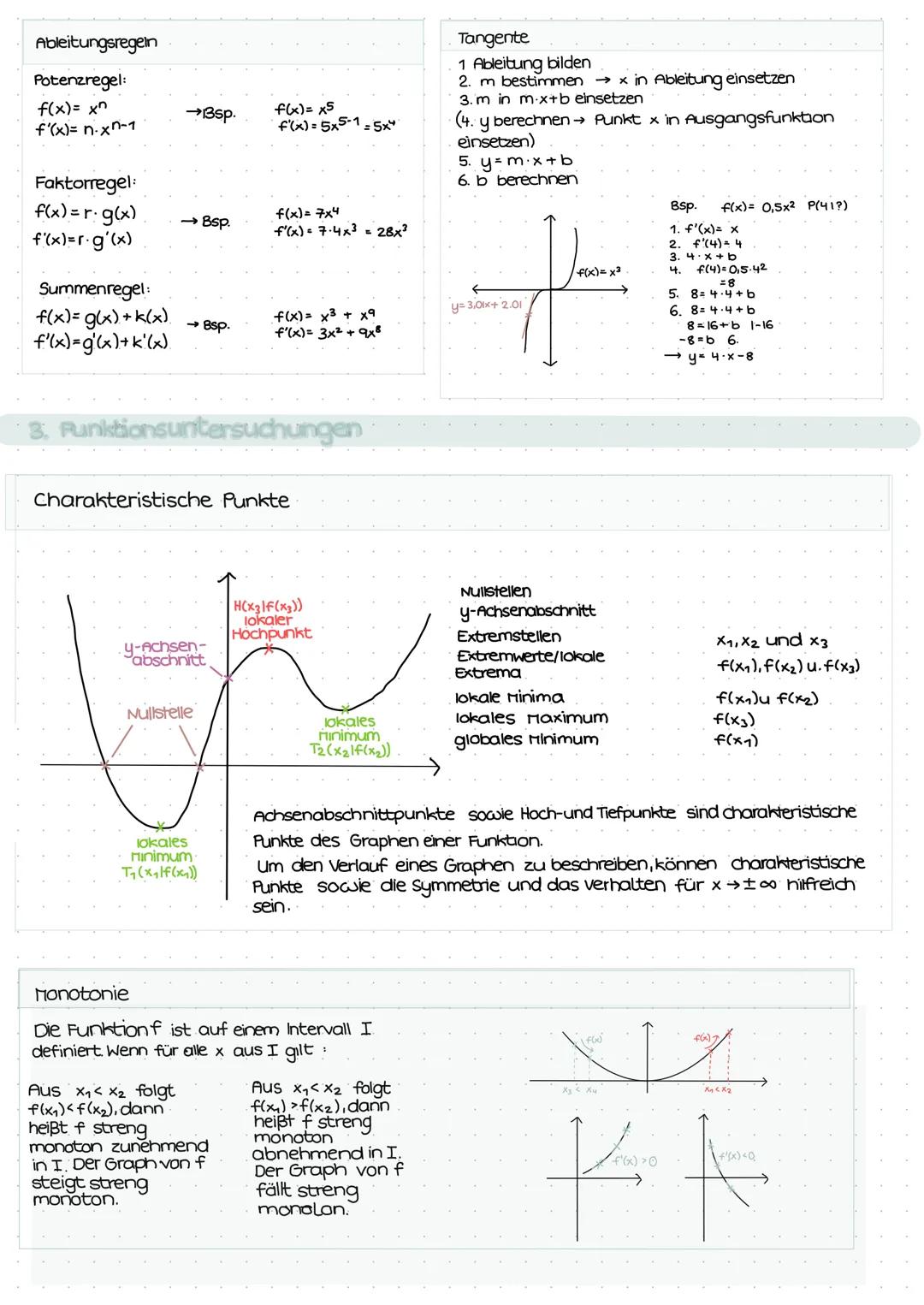
Charakteristische Punkte wie Nullstellen, y-Achsenabschnitt und Extrempunkte beschreiben den Graphenverlauf vollständig. Den y-Achsenabschnitt findest du durch f(0), Nullstellen durch f(x) = 0.
Monotonie beschreibt, ob eine Funktion steigt oder fällt. Mit dem Monotoniesatz prüfst du das über die Ableitung: f'(x) > 0 → streng monoton steigend, f'(x) < 0 → streng monoton fallend.
Extrempunkte findest du in zwei Schritten: Erst f'(x) = 0 lösen (notwendige Bedingung), dann Vorzeichenwechsel der Ableitung prüfen (hinreichende Bedingung). Wechsel von + nach - = Hochpunkt, von - nach + = Tiefpunkt.
Die zweite Ableitung macht's noch einfacher: f''(x) > 0 → Tiefpunkt, f''(x) < 0 → Hochpunkt. Vergiss nicht, die y-Koordinaten durch Einsetzen in f(x) zu berechnen!
Strategie: Immer systematisch vorgehen - erst notwendige, dann hinreichende Bedingung prüfen!