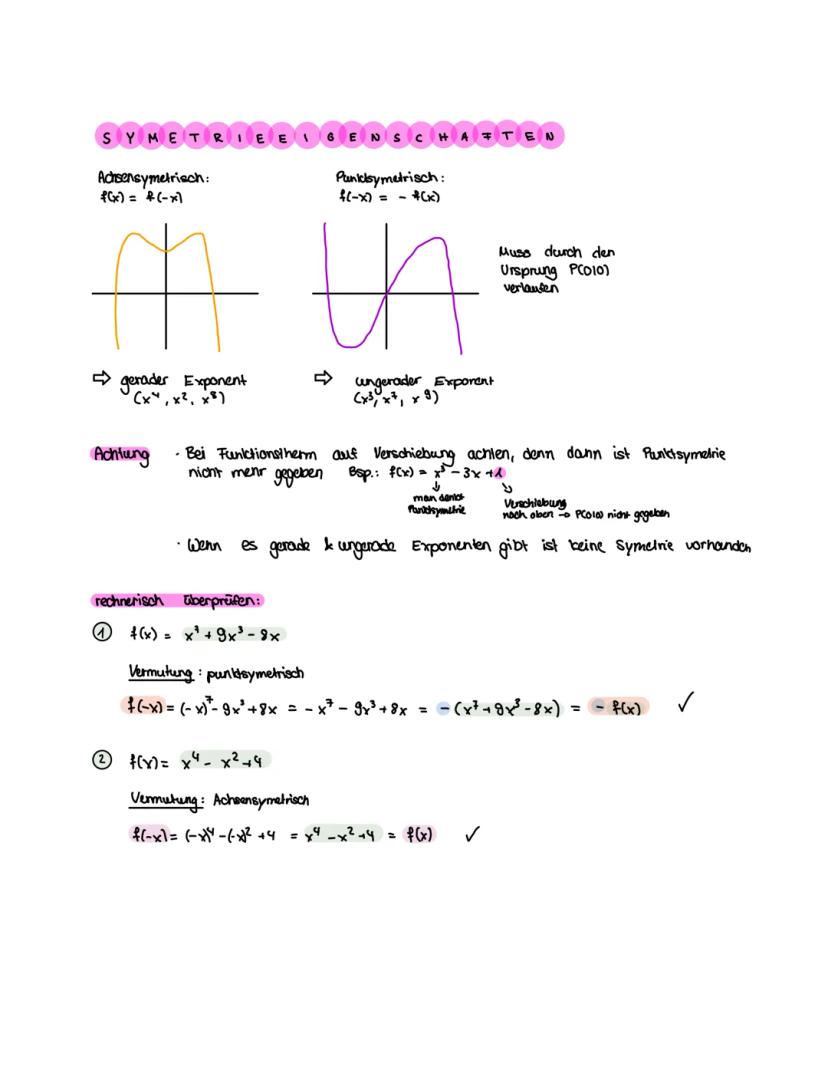
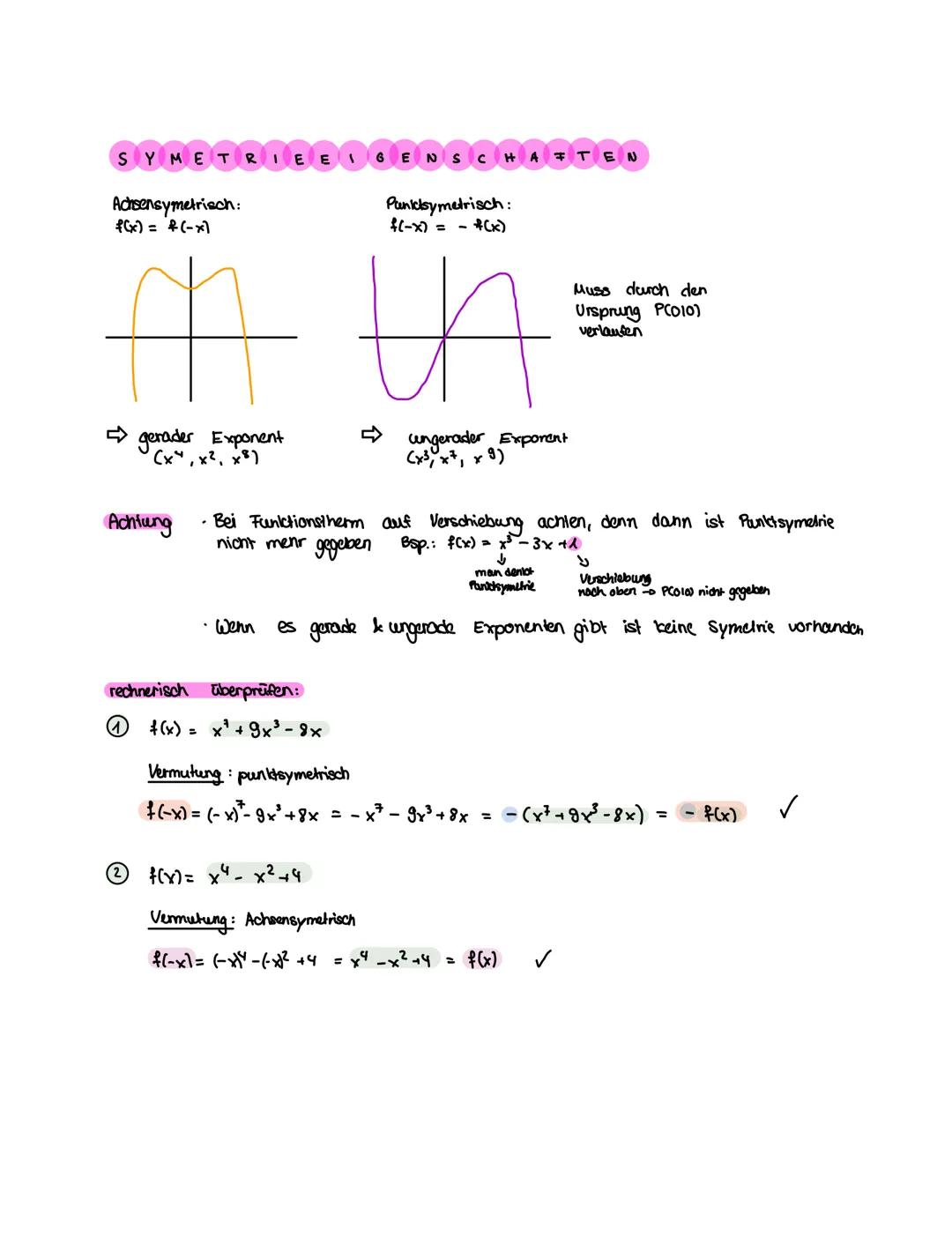
Ableitungsregeln und Besonderheiten

Ableitungen zeigen dir die Steigung einer Funktion an jedem Punkt. Mit den richtigen Regeln wird das Ableiten zum Kinderspiel!

Die Potenzregel ist dein bester Freund: f(x) = x^n wird zu f'(x) = n·x^$n-1$. Bei der Faktorregel bleibt der Faktor erhalten, und die Summenregel bedeutet einfach: jeden Term einzeln ableiten.

Besondere Fälle, die oft in Klassenarbeiten auftauchen: f(x) = x wird zu f'(x) = 1, und √x wird zu 1/(2√x). Bei Brüchen wie 2/x³ schreibst du zuerst 2x^(-3) und leitest dann ab: -6x^(-4).

Merktipp: Bei trigonometrischen Funktionen gilt: sin(x) → cos(x) und cos(x) → -sin(x)

Tangenten- und Normalengleichung

Du kennst das: Gegeben ist eine Funktion und ein Punkt, gesucht ist die Tangentengleichung. Das schaffst du in drei einfachen Schritten.

Zuerst bestimmst du die Steigung m durch die Ableitung an der Stelle x₀. Dann setzt du in die Geradengleichung t(x) = mx + b ein und löst nach b auf: b = f(x₀) - m·x₀.

Die Normale steht senkrecht zur Tangente. Hier gilt: m₂ = -1/m₁, wobei m₁ die Tangentensteigung ist. Der Rest funktioniert genauso wie bei der Tangente.

Wichtig: Normale und Tangente schneiden sich immer im rechten Winkel - das ist der Schlüssel zum Verständnis!

Ganzrationale Funktionen - Grundlagen

Ganzrationale Funktionen begegnen dir überall in der Mathematik. Sie bestehen aus Summen von Potenzen mit natürlichen Exponenten - keine negativen oder gebrochenen Exponenten erlaubt!

Der Grad einer Funktion ist der höchste Exponent, dessen Koeffizient nicht null ist. Bei f(x) = -x⁷ + 3x⁵ - x² + 2x - 4 ist das Grad 7. Die Zahlen vor den x-Potenzen heißen Koeffizienten.

Der Globalverlauf hängt nur vom höchsten Term ab. Bei geradem Grad verlaufen beide Enden in dieselbe Richtung, bei ungeradem Grad in entgegengesetzte Richtungen. Das Vorzeichen des führenden Koeffizienten entscheidet über die konkrete Richtung.

Eselsbrücke: Gerader Grad = beide Arme hoch oder runter, ungerader Grad = ein Arm hoch, einer runter!

Symmetrie von Funktionen

Symmetrieeigenschaften zu erkennen spart dir viel Arbeit beim Zeichnen und Rechnen. Es gibt zwei wichtige Typen: Achsen- und Punktsymmetrie.

Achsensymmetrie zur y-Achse liegt vor, wenn f$-x$ = f(x) gilt. Das passiert, wenn nur gerade Exponenten auftreten (x², x⁴, x⁶...). Punktsymmetrie zum Ursprung erkennst du an f$-x$ = -f(x) - hier sind nur ungerade Exponenten im Spiel.

Achtung: Wenn sowohl gerade als auch ungerade Exponenten vorkommen, ist keine Symmetrie vorhanden. Bei Verschiebungen (konstante Terme ≠ 0) geht die Punktsymmetrie zum Ursprung verloren.

Prüftipp: Setze einfach -x für x ein und schaue, was rauskommt - das verrät dir sofort die Symmetrie!

Nullstellenbestimmung

Nullstellen zu finden ist oft der Schlüssel zur Lösung. Je nach Form der Funktion hast du verschiedene Strategien zur Verfügung.

Bei faktorisierter Form wie f(x) = $x-2$·$x+3$ liest du die Nullstellen direkt ab: x₁ = 2 und x₂ = -3. Jeder Faktor wird null gesetzt und aufgelöst.

Für quadratische Terme verwendest du die pq-Formel oder Termumformungen wie das Ausklammern. Bei komplizierteren Funktionen höheren Grades suchst du oft zuerst nach rationalen Nullstellen durch Probieren.

Wichtig: Beim Wurzelziehen entstehen immer zwei Lösungen (+/-) - vergiss die negative nicht!