Differenzen- und Differentialquotient

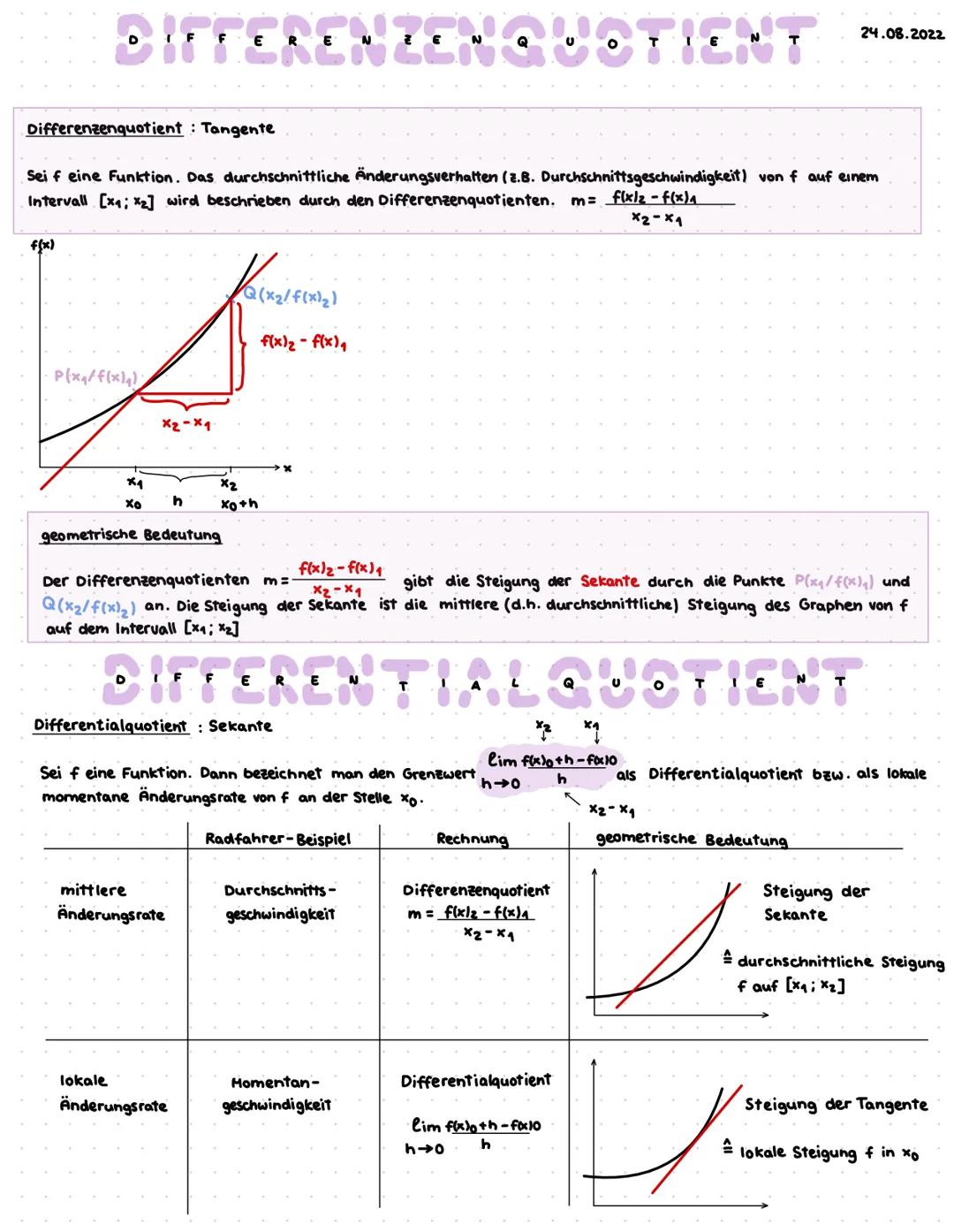
Stell dir vor, du fährst Fahrrad und willst wissen, wie schnell du warst. Der Differenzenquotient ist wie deine Durchschnittsgeschwindigkeit über eine bestimmte Strecke. Die Formel dafür ist: $m = \frac{f(x_2) - f(x_1)}{x_2 - x_1}$

Geometrisch betrachtet gibt dir dieser Wert die Steigung der Sekante an - das ist die gerade Linie, die zwei Punkte auf dem Graphen verbindet. Diese Sekante zeigt dir die mittlere Steigung des Graphen zwischen den beiden Punkten.

Der Differentialquotient hingegen ist wie deine Momentangeschwindigkeit zu einem ganz bestimmten Zeitpunkt. Er wird berechnet mit: $\lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}$. Das bedeutet, wir schauen uns an, was passiert, wenn der Abstand h immer kleiner wird.

Merktipp: Differenzenquotient = Durchschnitt über eine Strecke, Differentialquotient = genauer Moment an einem Punkt!

Geometrisch entspricht der Differentialquotient der Steigung der Tangente - also der Linie, die den Graphen nur an einem Punkt berührt. Diese zeigt dir die lokale Steigung genau an der Stelle x₀.