Grafisches Ableiten - So erkennst du Steigungen visuell
Grafisches Ableiten macht Mathe richtig anschaulich! Die Ableitungsfunktion f' zeigt dir nämlich genau, wie steil der Graph an jeder Stelle ist.
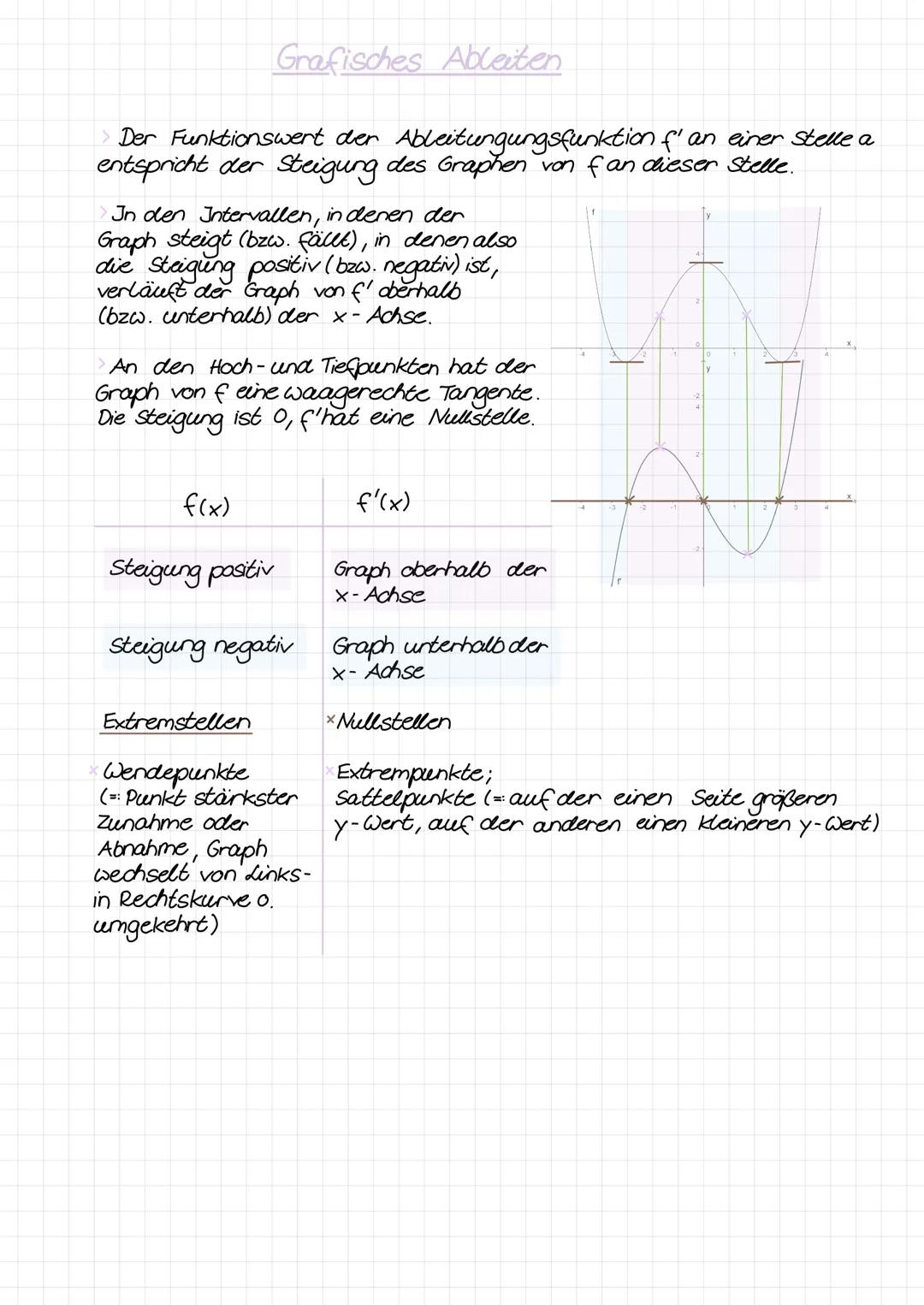
Wenn der ursprüngliche Graph nach oben steigt, ist die Steigung positiv - dann verläuft f' oberhalb der x-Achse. Fällt der Graph, ist die Steigung negativ und f' liegt unterhalb der x-Achse. So einfach ist das!
An Hoch- und Tiefpunkten wird's besonders interessant: Hier hat der Graph eine waagerechte Tangente, die Steigung ist also null. Das bedeutet, dass f' genau dort eine Nullstelle hat.
Wendepunkte sind die Stellen mit der stärksten Zu- oder Abnahme - hier wechselt der Graph von einer Links- in eine Rechtskurve oder umgekehrt. In der Ableitungsfunktion erkennst du sie an den Extrempunkten.
Merktipp: Positive Steigung = f' über der x-Achse, negative Steigung = f' unter der x-Achse!