Grundlagen des Integrals

Das Integral hilft dir, die Gesamtänderung einer Größe zu rekonstruieren, wenn du ihre momentane Änderungsrate kennst. Stell dir einen Tank vor, der befüllt und entleert wird - mit dem Integral kannst du den Füllstand zu jedem Zeitpunkt bestimmen.

Bei Funktionen, die nicht aus geradlinigen Teilstücken bestehen, nähert man den Flächeninhalt mit immer mehr Teilstücken an. Je mehr Teilstücke du verwendest, desto genauer wird die Annäherung. Diese Annäherungen von oben und unten streben gegen denselben Grenzwert - wenn dieser Grenzwert eindeutig ist, nennt man die Funktion integrierbar.

Der orientierte Flächeninhalt wird als Integral bezeichnet und mit dem Symbol $\int_a^b f(x)dx$ dargestellt. "Orientiert" bedeutet, dass Flächen oberhalb der x-Achse positiv und unterhalb negativ gezählt werden.

Merke: Das Integral $\int_a^b f(x)dx$ berechnet den Flächeninhalt zwischen dem Graphen von f, der x-Achse und den vertikalen Linien bei x=a und x=b.

Differenzial- und Integralrechnung

Der Hauptsatz der Differenzial- und Integralrechnung verbindet beide Bereiche: Ist F eine Stammfunktion von f $also F'(x) = f(x)$, dann gilt für das bestimmte Integral: $\int_a^b f(x)dx = F(b)-F(a)$. Diese Differenz schreibt man auch kompakt als $[F(x)]_a^b$.

Beim Integrieren gelten wichtige Rechenregeln:

• Linearität: Konstanten kannst du aus dem Integral ziehen und Summen aufteilen
• Intervalladditivität: Mehrere Integrale mit angrenzenden Intervallen kannst du zu einem Integral zusammenfassen

Die Beziehung zwischen Funktion und Stammfunktion kannst du grafisch verstehen: Wo f(x) eine Nullstelle mit Vorzeichenwechsel hat, besitzt F(x) eine Extremstelle. Wo f(x) eine Extremstelle hat, hat F(x) einen Wendepunkt. Diese NEW-Regel hilft dir, den Zusammenhang zwischen einer Funktion und ihrer Stammfunktion zu visualisieren.

Tipp: Denk immer daran: Ableiten und Integrieren sind Gegensätze - was beim Ableiten wegfällt (z.B. Konstanten), musst du beim Integrieren wieder hinzufügen!

Stammfunktionen bestimmen

Die Potenzregel ist dein wichtigstes Werkzeug beim Integrieren: Für $f(x) = x^r$ ist die Stammfunktion $F(x) = \frac{1}{r+1} \cdot x^{r+1}$. Du erhöhst also den Exponenten um 1 und teilst durch diesen neuen Exponenten.

Beispiele für die Potenzregel:

• $f(x) = x \Rightarrow F(x) = \frac{1}{2}x^2$
• $f(x) = x^2 \Rightarrow F(x) = \frac{1}{3}x^3$
• $f(x) = 2x^2 \Rightarrow F(x) = \frac{2}{3}x^3$

Bei ganzrationalen Funktionen wendest du die Potenzregel auf jeden Summanden einzeln an. Bei trigonometrischen Funktionen gilt: sin(x) wird zu -cos(x) und cos(x) wird zu sin(x). Die e-Funktion bleibt beim Integrieren unverändert: $f(x) = e^x \Rightarrow F(x) = e^x$.

Für komplexere Funktionen nutzt du die lineare Substitution:

1. Bestimme die innere und äußere Funktion
2. Bilde die Stammfunktion der äußeren Funktion
3. Dividiere durch die Ableitung der inneren Funktion

Vereinfache deinen Ansatz: Vor dem Integrieren solltest du die Funktion in eine Form bringen, die du gut kennst - etwa durch Umformen von Brüchen in Potenzfunktionen mit negativen Exponenten.

Gebrochenrationale Funktionen und Integralfunktionen

Bei gebrochenrationalen Funktionen wandelst du den Bruch in eine Form mit negativem Exponenten um: $f(x) = \frac{1}{x} = x^{-1}$. Ein Sonderfall ist $f(x) = \frac{1}{x}$, dessen Stammfunktion $F(x) = \ln|x|$ ist.

Warum steht hier der Betrag? Beim Ableiten von ln(x) braucht man keinen Betrag, da der Definitionsbereich auf positive Zahlen beschränkt ist. Beim Integrieren benötigen wir den Betrag, damit wir auch negative x-Werte einsetzen können.

Die Integralfunktion (auch unbestimmtes Integral genannt) beschreibt das Integral von einer festen unteren Grenze u bis zu einer variablen oberen Grenze x: $J_u(x) = \int_u^x f(t)dt$. Wichtige Eigenschaften:

• $J_u'(x) = f(x)$, d.h. die Integralfunktion ist eine Stammfunktion
• $J_u(u) = 0$, d.h. die untere Grenze ist stets eine Nullstelle der Integralfunktion

Der Unterschied zur Stammfunktion: Die Integralfunktion berechnet das Integral von einer festen Stelle bis zu einer variablen Stelle, während das unbestimmte Integral die Menge aller Stammfunktionen angibt.

Praktischer Tipp: Wenn du nach einer oberen Grenze x gefragt wirst, für die das Integral einen bestimmten Wert hat, setze diesen Wert ein und löse die entstehende Gleichung nach x auf.

Flächenberechnung mit Integralen

Bei der Berechnung von Flächeninhalten musst du auf das Vorzeichen achten:

• Beim orientierten Flächeninhalt zählen Flächen oberhalb der x-Achse positiv und unterhalb negativ
• Beim Gesamtflächeninhalt berechnest du alle Flächen als positive Werte

Liegt eine Fläche teilweise unter der x-Achse, gehe so vor:

1. Bestimme die Nullstellen der Funktion
2. Berechne die Teilflächen und addiere deren Beträge: $A = |\int_a^s f(x)dx| + |\int_s^b f(x)dx|$

Für die Fläche zwischen zwei Graphen $f(x)$ und $g(x)$ im Intervall [a,b] verwendest du: $A = \int_a^b (f(x)-g(x))dx$ für $f(x) \geq g(x)$ im gesamten Intervall

Falls nicht bekannt ist, welcher Graph oberhalb liegt, musst du den Betrag nehmen: $A = |\int_a^b (f(x)-g(x))dx|$

Beachte: Bei der Flächenberechnung zwischen zwei Graphen musst du zuerst die Schnittpunkte bestimmen und dann die Integrale für die einzelnen Teilbereiche aufstellen, in denen jeweils eine Funktion über der anderen liegt.

Der Mittelwert einer Funktion

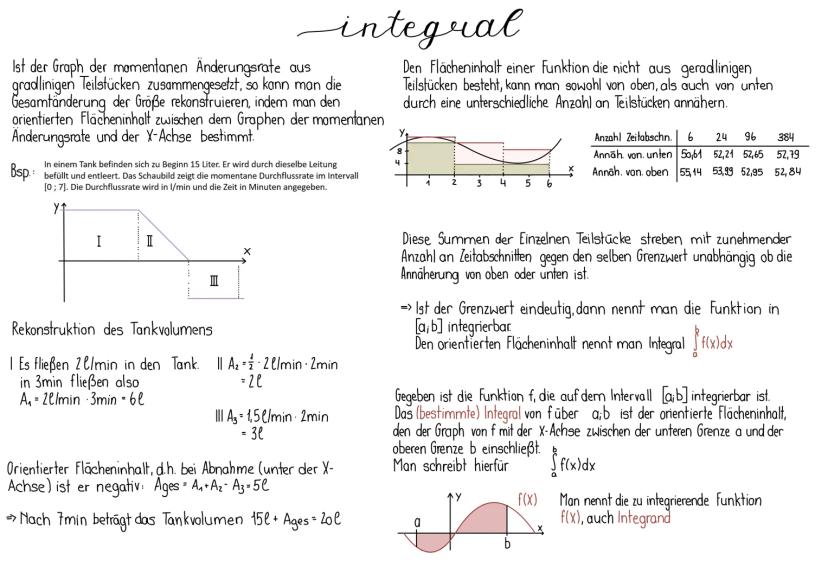
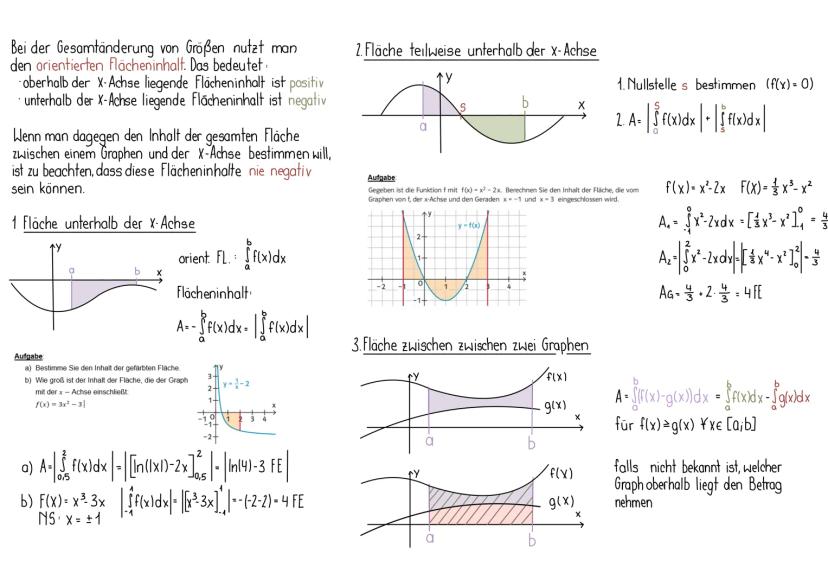
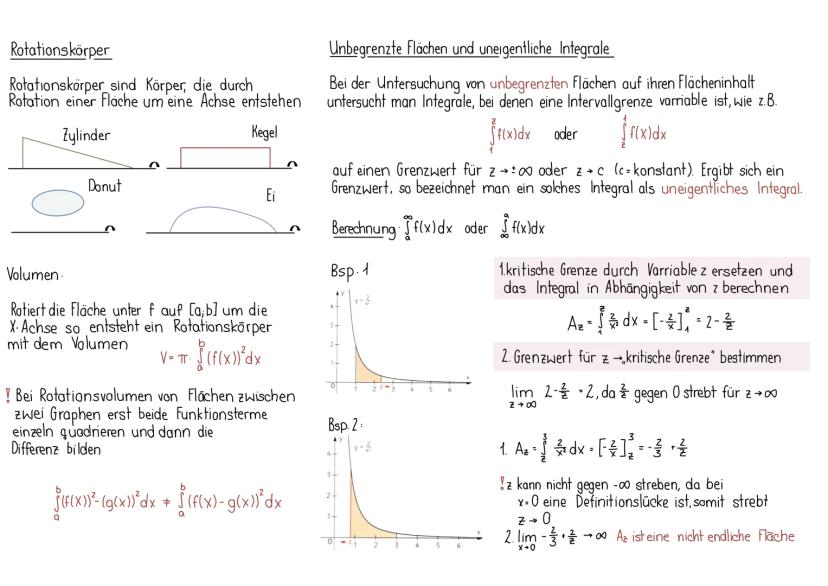
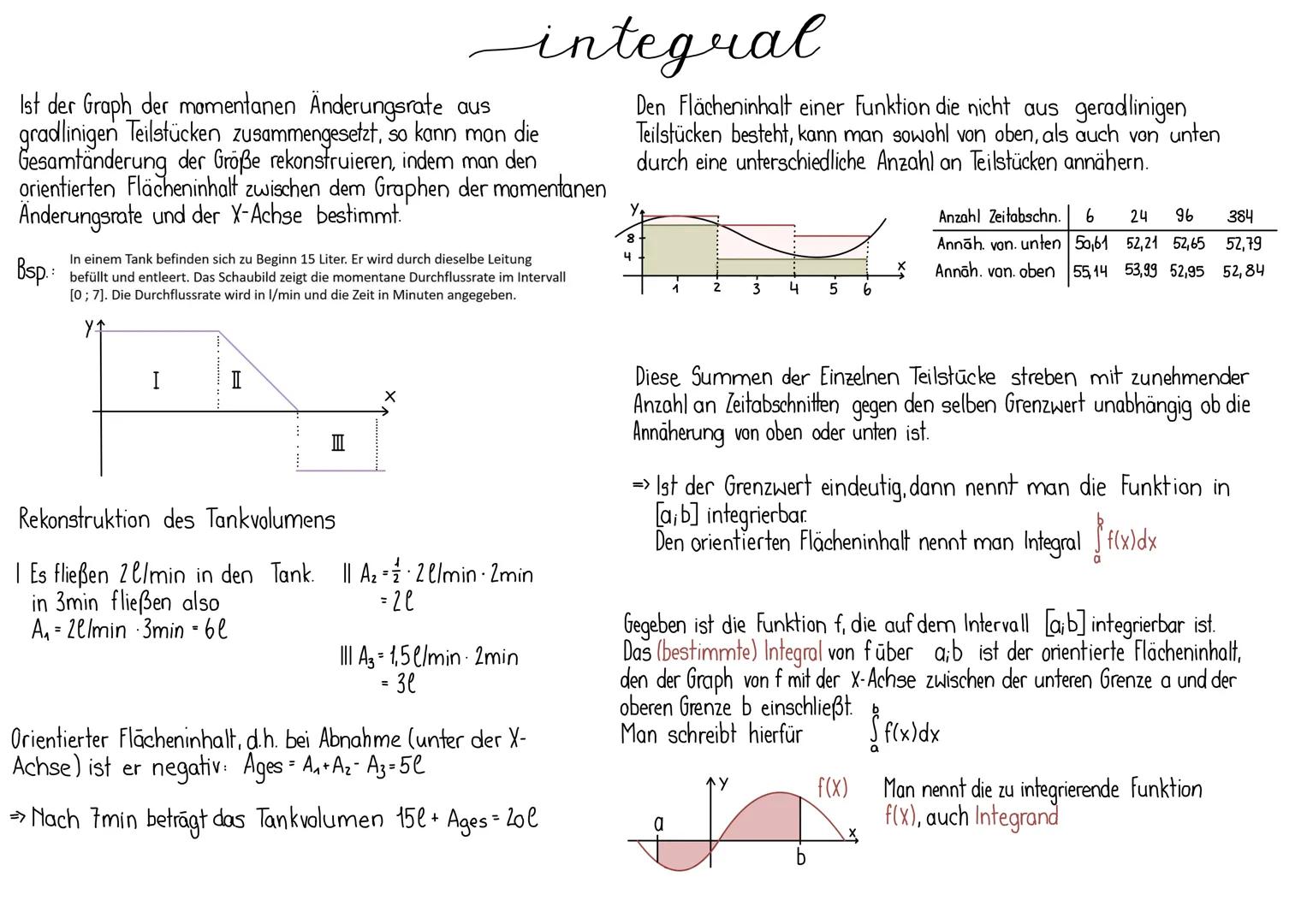
Bei endlich vielen Werten kennst du bereits den arithmetischen Mittelwert: Die Summe aller Werte geteilt durch ihre Anzahl. Aber wie berechnet man den Mittelwert einer Funktion, die unendlich viele Werte hat?

Der Mittelwert einer Funktion f im Intervall [a,b] wird definiert als: $m = \frac{1}{b-a} \cdot \int_a^b f(x)dx$

Praktische Bedeutung: Der Mittelwert gibt an, welchen konstanten Wert die Funktion haben müsste, um im gleichen Intervall den gleichen Flächeninhalt zu ergeben. Bei einer Quelle bedeutet dies zum Beispiel, wie viel Wasser gleichmäßig abgegeben werden müsste, um dieselbe Gesamtmenge zu erhalten.

Grafisch kannst du dir den Mittelwert als horizontale Linie vorstellen, bei der die Flächen A₁ (über der Linie) und A₂ (unter der Linie) gleich groß sind. Diese horizontale Linie teilt also die Fläche zwischen Funktionsgraph und x-Achse in zwei gleichgroße Teile.

Anschaulich betrachtet: Der Mittelwert einer Funktion ist die Höhe des Rechtecks, das dieselbe Breite und denselben Flächeninhalt hat wie die Fläche unter dem Funktionsgraphen.

Rotationskörper und uneigentliche Integrale

Rotationskörper entstehen, wenn eine Fläche um eine Achse rotiert. Bekannte Beispiele sind Kegel, Zylinder, Donuts oder Eiform. Das Volumen eines Rotationskörpers, der durch Rotation der Fläche unter f(x) im Intervall [a,b] um die x-Achse entsteht, berechnet sich mit: $V = \pi \cdot \int_a^b (f(x))^2 dx$

Bei Flächen zwischen zwei Funktionen $f(x)$ und $g(x)$ musst du beachten: $V = \pi \cdot \int_a^b ((f(x))^2 - (g(x))^2) dx$

Uneigentliche Integrale behandeln unbegrenzte Flächen, bei denen mindestens eine Intervallgrenze ins Unendliche geht oder eine Definitionslücke vorliegt. Die Berechnung erfolgt in zwei Schritten:

1. Ersetze die kritische Grenze durch eine Variable z und berechne das Integral in Abhängigkeit von z
2. Bestimme den Grenzwert für z gegen die kritische Grenze (z.B. z → ∞)

Wichtiger Hinweis: Bei Rotationsvolumen zwischen zwei Graphen musst du beide Funktionsterme einzeln quadrieren und dann die Differenz bilden. Der Ausdruck $\int_a^b (f(x) - g(x))^2 dx$ liefert ein falsches Ergebnis!