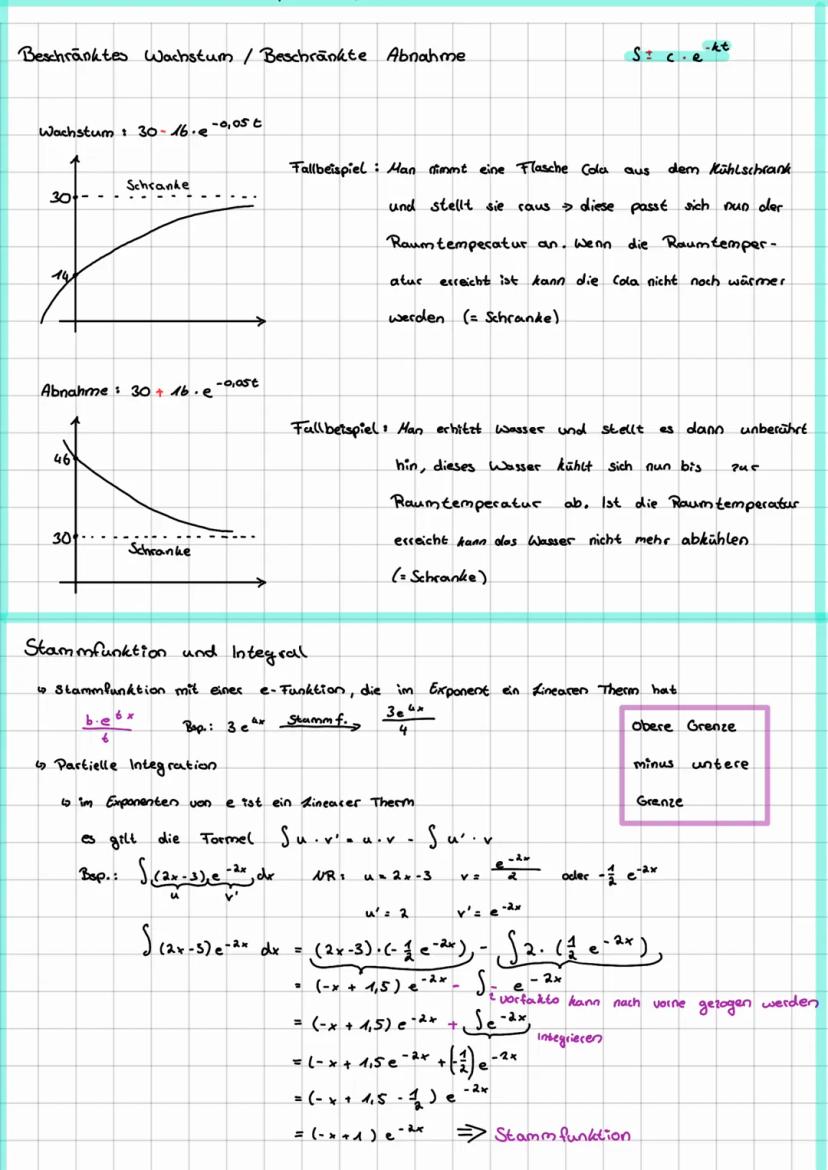
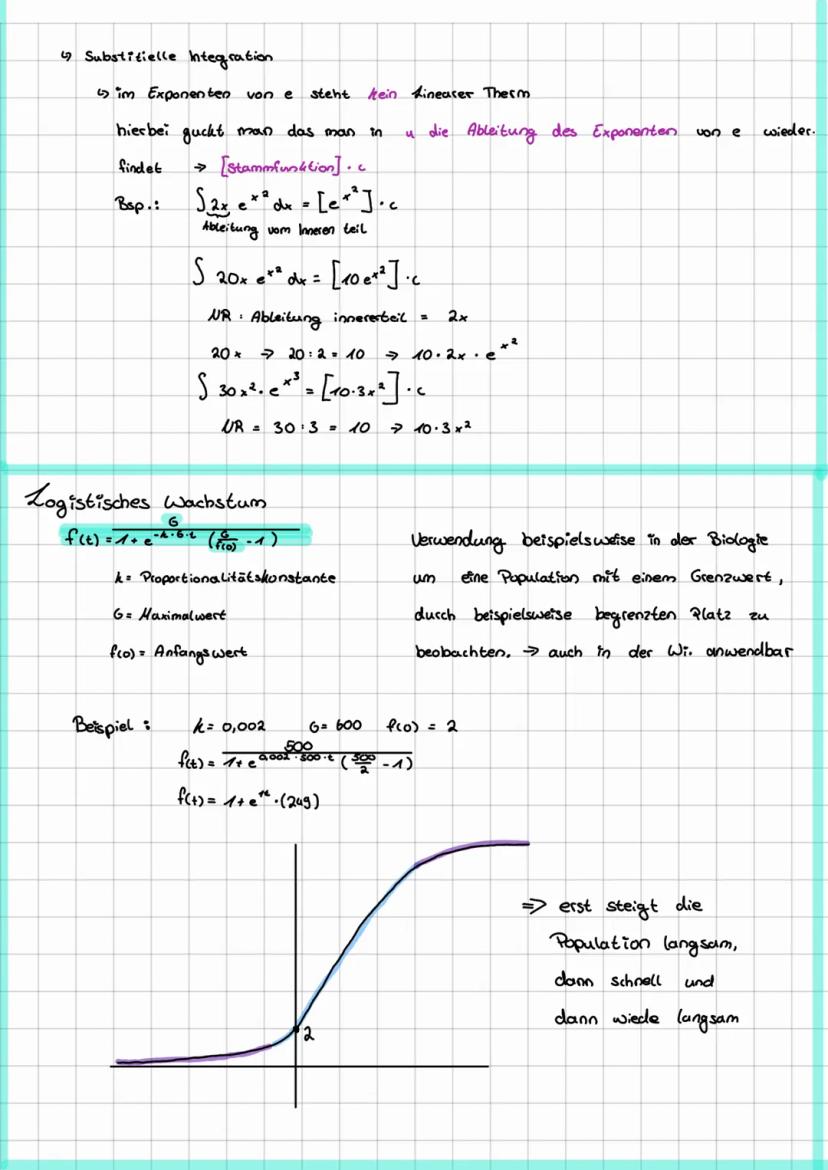
Grundlagen der e-Funktion

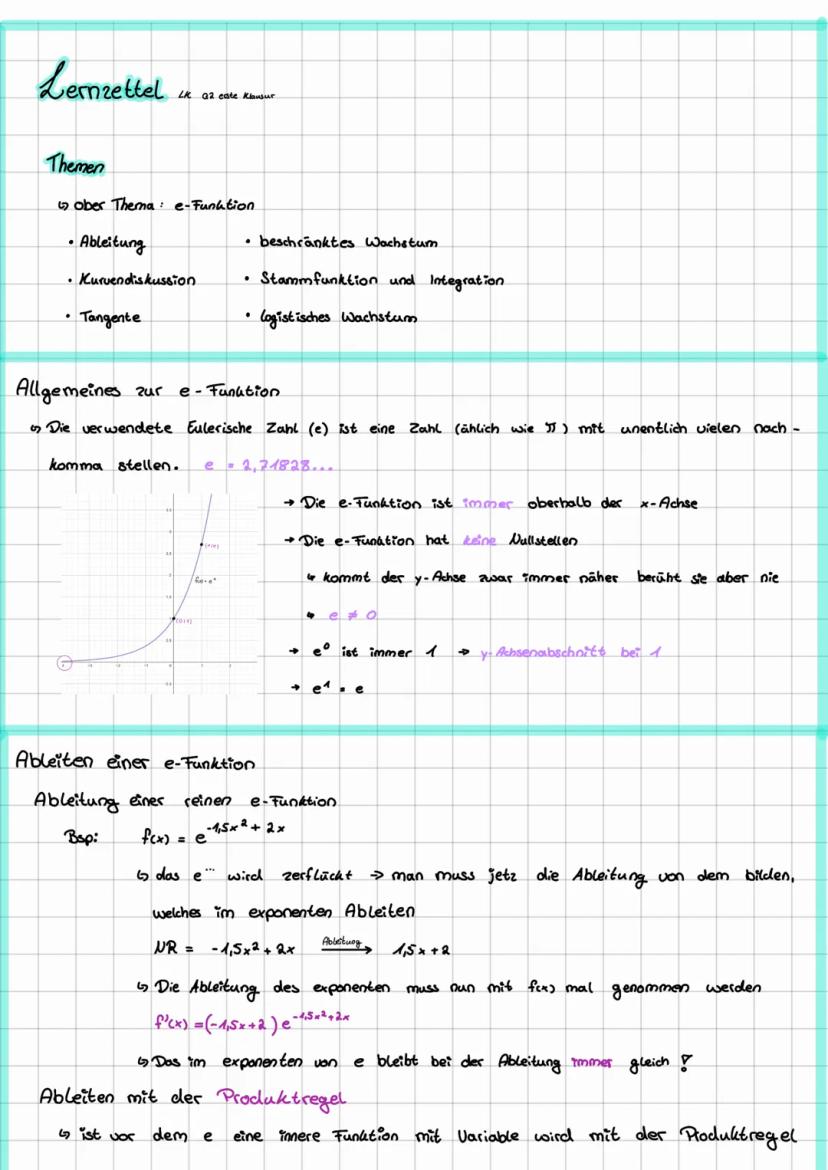
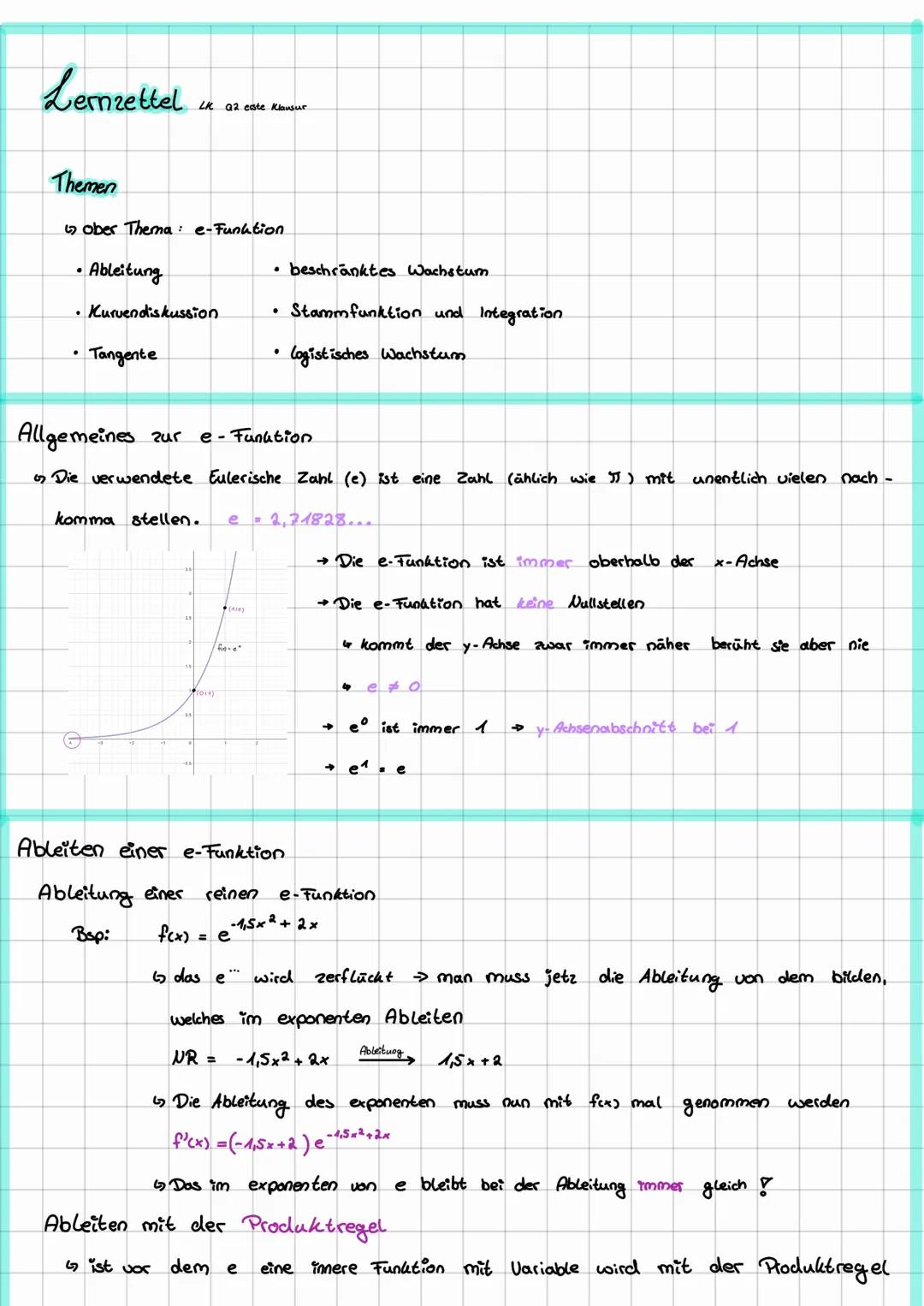
Die e-Funktion hat einige coole Eigenschaften, die du dir unbedingt merken solltest. Die Eulersche Zahl e = 2,71828... ist wie π eine irrationale Zahl mit unendlich vielen Nachkommastellen.

Das Wichtigste: Die e-Funktion ist immer positiv! Sie liegt komplett oberhalb der x-Achse und hat deshalb keine Nullstellen. Links nähert sie sich der x-Achse zwar unendlich an, berührt sie aber nie.

Beim Ableiten wird's richtig praktisch. Wenn du eine reine e-Funktion wie f$x$ = e^$-1,5x² + 2x$ ableitest, bleibt das e komplett unverändert. Du leitest nur den Exponenten ab und multiplizierst das Ergebnis mit der ursprünglichen Funktion: f'$x$ = $-3x + 2$ · e^$-1,5x² + 2x$.

Merktipp: Bei e-Funktionen bleibt der Exponent beim Ableiten immer gleich - du rechnest nur mit der Ableitung des Exponenten weiter!

Ableitung mit Produktregel und Kurvendiskussion

Wenn vor dem e noch eine andere Funktion steht, brauchst du die Produktregel: (u·v)' = u'·v + u·v'. Du teilst einfach den Teil vor dem e $= u$ und den e-Teil $= v$ auf, leitest beide getrennt ab und setzt in die Formel ein.

Bei der Kurvendiskussion wird's easy: Wenn du e-Funktionen gleich null setzt, kannst du das e einfach wegstreichen! Da e nie null wird, musst du nur den anderen Teil der Funktion betrachten.

Tangenten berechnen funktioniert wie immer: Du brauchst einen Punkt (x-Wert einsetzen) und die Steigung (erste Ableitung). Mit y = mx + b findest du dann deine Tangentengleichung.

Praxistipp: Bei Kurvendiskussionen von e-Funktionen ignorierst du das e beim Nullsetzen - es kann eh nicht null werden!

Beschränktes Wachstum und Integration

Beschränktes Wachstum siehst du überall im Alltag! Deine Cola aus dem Kühlschrank erwärmt sich bis zur Raumtemperatur, aber nicht darüber hinaus - das ist die Schranke. Die Formel dafür: f$t$ = Schranke ± c·e^$-kt$.

Bei Wachstum steht ein Minus vor dem c, bei Abnahme ein Plus. Die Schranke ist der Wert, dem sich die Funktion immer weiter annähert, aber nie überschreitet.

Für die Integration gibt's zwei wichtige Methoden. Bei linearen Exponenten verwendest du die Formel ∫ b·e^(ax) dx = (b/a)·e^(ax) + C. Bei komplizierteren Exponenten brauchst du die partielle Integration: ∫ u·v' = u·v - ∫ u'·v.

Alltagsbezug: Beschränktes Wachstum erklärt, warum dein Handy-Akku am Anfang schnell lädt und zum Ende hin immer langsamer wird!

Substitution und logistisches Wachstum

Substitutionsmethode verwendest du, wenn im Exponenten kein linearer Term steht. Der Trick: Du suchst die Ableitung des Exponenten in der Funktion und teilst entsprechend. Bei ∫ 2x·e^(x²) dx ist die Ableitung von x² genau 2x - perfekt!

Falls der Faktor nicht passt, rechnest du ihn einfach raus: ∫ 20x·e^(x²) dx = 10·∫ 2x·e^(x²) dx = 10·e^(x²) + C.

Logistisches Wachstum beschreibt realistisches Wachstum mit Grenzen: f$t$ = G/$1 + e^(-k(t-t₀))$. Dabei ist G der Maximalwert und k die Wachstumsrate.

Die Kurve sieht aus wie ein liegendes S: erst langsames Wachstum, dann schneller Anstieg, schließlich wieder Verlangsamung bis zum Maximum. Das erklärt Bevölkerungswachstum, Virenausbreitung oder Marktdurchdringung neuer Produkte.

Realitätsbezug: Logistisches Wachstum zeigt, warum TikTok-Trends erst langsam starten, dann explodieren und schließlich wieder abflachen!