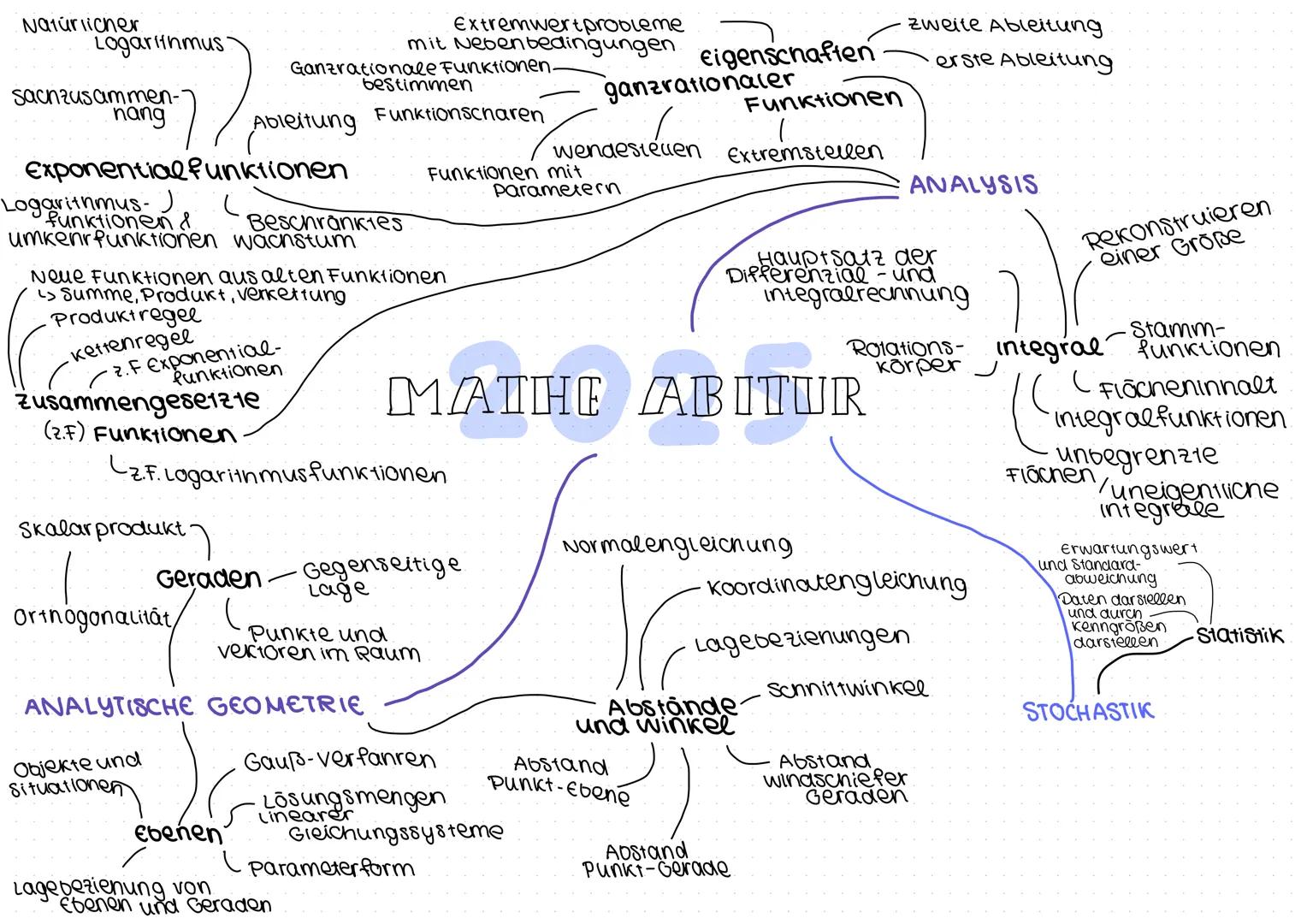
Mathe-Abitur Übersicht - Die drei großen Bereiche
Analysis ist der Bereich, in dem du dich hauptsächlich mit Funktionen beschäftigst. Hier lernst du ganzrationale Funktionen, Exponentialfunktionen und Logarithmusfunktionen kennen und analysieren.
Die erste Ableitung hilft dir dabei, Extremstellen zu finden, während die zweite Ableitung Wendestellen aufspürt. Bei Funktionscharen kommen Parameter ins Spiel, die das Verhalten der Funktion beeinflussen.
Integralrechnung ist das Gegenstück zur Ableitung - hier berechnest du Flächeninhalte und Rotationskörper. Der Hauptsatz der Differential- und Integralrechnung verbindet beide Bereiche elegant miteinander.
Tipp: Lerne Produktregel und Kettenregel auswendig - die brauchst du ständig bei zusammengesetzten Funktionen!
Analytische Geometrie arbeitet mit Punkten und Vektoren im Raum. Du beschreibst Geraden in Parameterform und Ebenen sowohl in Parameter- als auch in Koordinatengleichung.
Lagebeziehungen, Abstände und Schnittwinkel sind die Kernthemen hier. Das Skalarprodukt ist dein wichtigstes Werkzeug für Berechnungen zur Orthogonalität.
Stochastik umfasst Statistik und Wahrscheinlichkeitsrechnung. Du lernst, Daten darzustellen und durch Kenngrößen wie Erwartungswert und Standardabweichung zu beschreiben.