Lernzettel Übersicht

Mathe GK Abitur 2025 - dein kompletter Wegweiser durch alle prüfungsrelevanten Themen! Die folgenden fünf Bereiche decken alles ab, was du fürs Abi brauchst.

Von den Grundlagen mit Gleichungen und binomischen Formeln bis hin zur Stochastik - jeder Bereich baut logisch auf dem anderen auf. Analysis und analytische Geometrie sind oft die Schwerpunkte im Abitur, deshalb solltest du hier besonders gut vorbereitet sein.

Die Funktionen verbinden alle Bereiche miteinander und sind das Herzstück der Oberstufen-Mathematik. Mit diesem strukturierten Lernzettel behältst du den Überblick und kannst gezielt deine Schwächen angehen.

Tipp: Arbeite die Themen in der angegebenen Reihenfolge durch - die Grundlagen brauchst du für alles Weitere!

Grundlagen

Gleichungen lösen ist wie ein Spiel mit festen Regeln - und die sind eigentlich total simpel! Bei Gleichungen auflösen gehst du immer systematisch vor: Klammern auflösen, zusammenfassen, dann alles mit Zahlen auf eine Seite und alles mit Buchstaben auf die andere.

Die binomischen Formeln sind deine besten Freunde beim Vereinfachen von Termen. $(a+b)^2 = a^2 + 2ab + b^2$ und $(a-b)^2 = a^2 - 2ab + b^2$ kommen ständig vor. Die dritte Formel $(a+b)(a-b) = a^2 - b^2$ ist besonders praktisch zum Faktorisieren.

Mit der pq-Formel $x_{1,2} = -\frac{p}{2} ± \sqrt{(\frac{p}{2})^2 - q}$ knackst du jede quadratische Gleichung. Bei der Prozentrechnung merkst du dir einfach: Prozentwert = Prozentsatz × Grundwert, dann kannst du die Formel nach jeder Größe umstellen.

Merksatz: Übung macht den Meister - diese Grundlagen brauchst du in jeder Abituraufgabe!

Funktionen

Ganzrationale Funktionen sind Funktionen ohne Wurzeln oder Brüche - nur Potenzen mit natürlichen Exponenten. Der höchste Exponent bestimmt den Grad der Funktion und damit ihr Verhalten für sehr große oder sehr kleine x-Werte.

Das Verhalten für x → ±∞ hängt nur vom Term mit der höchsten Potenz ab. Eine Funktion 3. Grades mit positivem Leitkoeffizienten geht links nach unten und rechts nach oben. Bei geraden Graden verhalten sich beide Seiten gleich.

Lineare Funktionen $f(x) = mx + b$ sind die einfachsten, quadratische Funktionen $f(x) = ax^2 + bx + c$ bilden Parabeln. Exponentialfunktionen $f(x) = c \cdot a^x$ wachsen oder fallen exponentiell - sie werden nie null und sind immer positiv.

Funktionsscharen enthalten einen Parameter (meist a), den du wie eine normale Zahl behandelst. Der Parameter verändert die Form oder Lage der Funktion.

Wichtig: Der Grad einer Funktion verrät dir sofort, wie viele Nullstellen und Extrempunkte maximal möglich sind!

Ableitungsregeln

Die Potenzregel ist dein Standardwerkzeug: Bei $f(x) = x^n$ wird $f'(x) = n \cdot x^{n-1}$ - einfach den Exponenten nach vorne holen und um eins verringern. Die Summenregel besagt: Du kannst jeden Summanden einzeln ableiten und dann addieren.

Bei der Kettenregel teilst du die Funktion in äußere und innere Funktion auf. Die Ableitung ist dann: äußere Ableitung mal innere Ableitung. Das brauchst du bei allen "Funktionen in Funktionen".

Die Produktregel verwendest du, wenn zwei Funktionen multipliziert werden: $f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)$. Die e-Funktion ist besonders: $f(x) = e^x$ hat die Ableitung $f'(x) = e^x$ - sie bleibt beim Ableiten unverändert!

Trick: Bei der e-Funktion mit Kettenregel: $f'(x) = e^{g(x)} \cdot g'(x)$ - die innere Ableitung nicht vergessen!

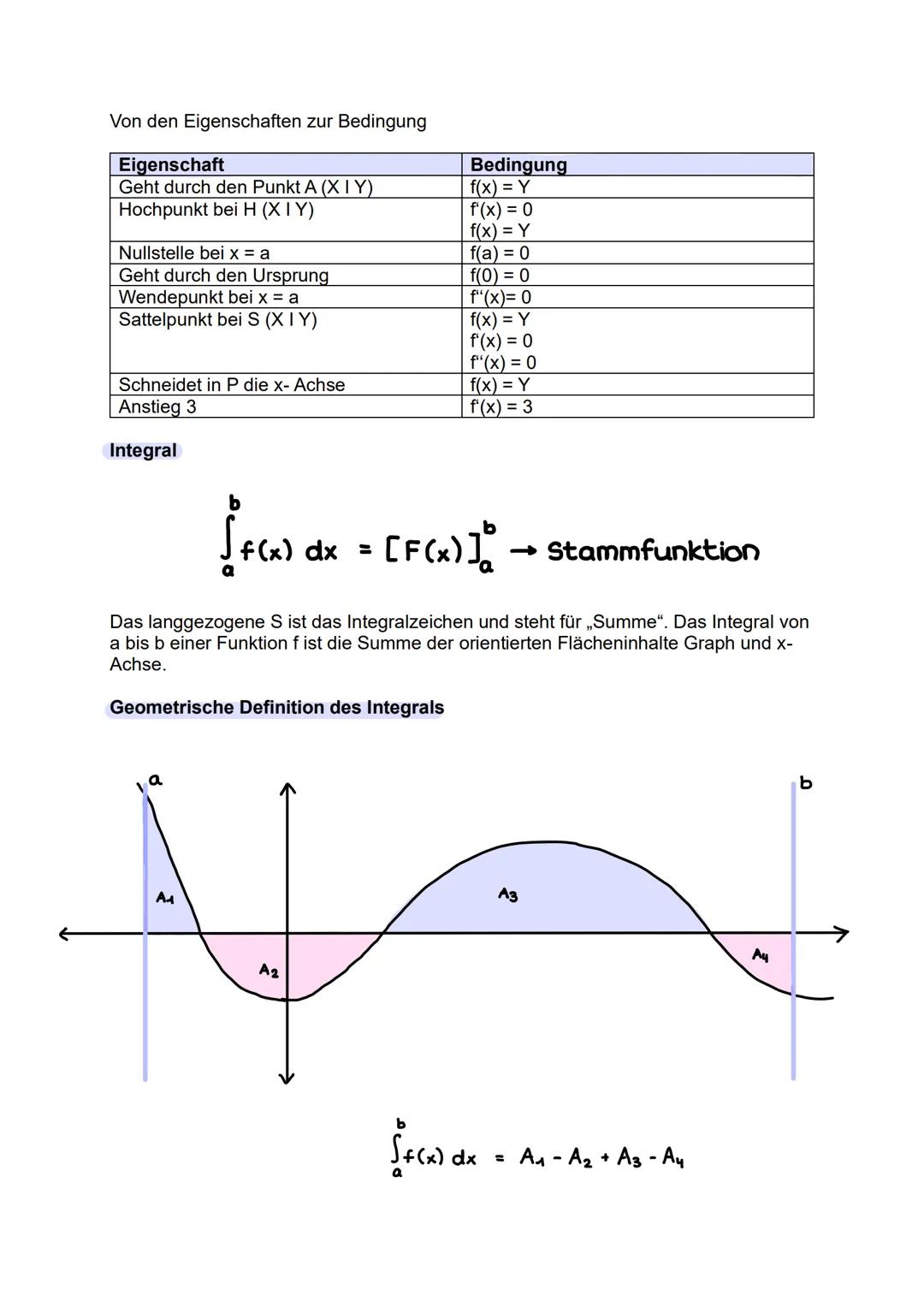
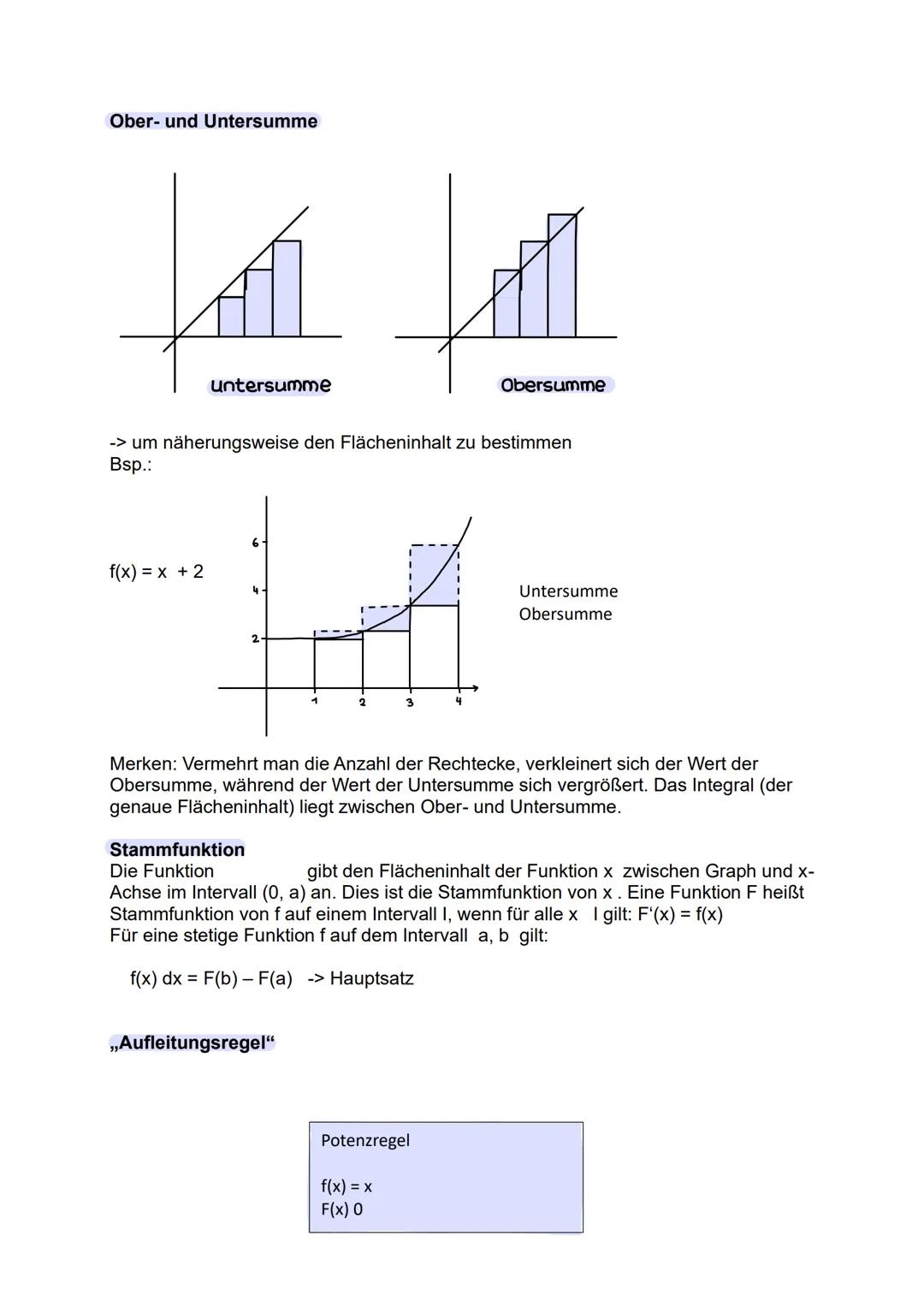
Analysis - Besondere Punkte

Der Monotoniesatz verrät dir, wo eine Funktion steigt oder fällt: Ist $f'(x) > 0$, steigt die Funktion; ist $f'(x) < 0$, fällt sie. An Nullstellen der ersten Ableitung können Extrempunkte liegen.

Hoch- und Tiefpunkte findest du in zwei Schritten: Erst $f'(x) = 0$ lösen (notwendige Bedingung), dann prüfen mit $f''(x)$ oder dem Vorzeichenwechselkriterium (hinreichende Bedingung). Bei $f''(x) > 0$ hast du einen Tiefpunkt, bei $f''(x) < 0$ einen Hochpunkt.

Wendepunkte sind Stellen, wo die Krümmung wechselt - dort ist $f''(x) = 0$. Nullstellen erhältst du durch $f(x) = 0$, den y-Achsenabschnitt durch Einsetzen von $x = 0$.

Diese charakteristischen Punkte helfen dir, den Funktionsgraph zu skizzieren und das Verhalten der Funktion vollständig zu beschreiben.

Eselsbrücke: f' = 0 für Extrema, f'' = 0 für Wendepunkte - erst die erste, dann die zweite Ableitung!

Funktionsverhalten und Steckbriefaufgaben

Das Verhalten für x → ±∞ bestimmst du immer über den Term mit der höchsten Potenz. Bei geraden Graden (2, 4, 6...) verhalten sich beide Seiten gleich, bei ungeraden Graden (1, 3, 5...) gegensätzlich.

Stetigkeit bedeutet, dass der Graph ohne Absetzen gezeichnet werden kann. Eine Funktion ist knickfrei, wenn die Ableitungen an der Stelle übereinstimmen, und sprungfrei, wenn die Funktionswerte übereinstimmen.

Bei Steckbriefaufgaben übersetzt du die gegebenen Eigenschaften in mathematische Gleichungen: "Nullstelle bei x = 2" wird zu $f(2) = 0$, "Hochpunkt bei (1|3)" wird zu $f(1) = 3$ und $f'(1) = 0$. Dann stellst du ein Gleichungssystem auf und löst es.

Strategie: Zähle zuerst die Bedingungen - du brauchst genauso viele wie unbekannte Parameter!

Integralrechnung Grundlagen

Ober- und Untersummen sind Rechtecke, die den Flächeninhalt näherungsweise bestimmen. Die Untersumme ist immer kleiner, die Obersumme immer größer als der echte Flächeninhalt. Je mehr Rechtecke, desto genauer wird die Näherung.

Eine Stammfunktion F(x) ist das Gegenteil der Ableitung: Wenn $F'(x) = f(x)$, dann ist F eine Stammfunktion von f. Der Hauptsatz der Integralrechnung besagt: $\int_a^b f(x) dx = F(b) - F(a)$.

Die Potenzregel fürs Integrieren: $\int x^n dx = \frac{x^{n+1}}{n+1} + C$ - Exponent um eins erhöhen und dadurch teilen. Die Summen- und Faktorregel funktionieren wie beim Ableiten.

Integrale haben viele praktische Bedeutungen: Geschwindigkeit → Wegstrecke, Wachstumsrate → Zuwachs, Wasserzuflussstärke → Wassermenge.

Merkhilfe: Integrieren ist "Aufleiten" - das Gegenteil vom Ableiten!

Integralrechnung - Rechenregeln und Flächenberechnung

Wichtige Rechenregeln für Integrale: $\int_a^a f(x) dx = 0$ (gleiche Grenzen), $\int_a^b f(x) dx = -\int_b^a f(x) dx$ (vertauschte Grenzen wechseln das Vorzeichen), und die Linearität: $\int_a^b (f(x) + g(x)) dx = \int_a^b f(x) dx + \int_a^b g(x) dx$.

Den Flächeninhalt zwischen zwei Graphen berechnest du mit $A = \int_a^b |f(x) - g(x)| dx$. Dabei ist es egal, auf welcher Höhe die Funktionen liegen - nur ihr Abstand zählt.

Die Faktorregel besagt: $\int c \cdot f(x) dx = c \cdot \int f(x) dx$ - Konstanten kannst du vor das Integral ziehen. Bei der Summenregel integrierst du jeden Summanden einzeln.

Praxistipp: Skizziere immer die Funktionen, um zu sehen, welche oben liegt - das bestimmt das Vorzeichen!

Exponentialfunktionen und Logarithmus

Den Wachstumsfaktor bestimmst du aus zwei Punkten: $a = \sqrt[x_2-x_1]{\frac{y_2}{y_1}}$ - oft ist der Bruch viel genauer als einzelne Berechnungen. Bei Exponentialgleichungen isolierst du erst den Exponentialterm, dann logarithmierst du.

Die e-Funktion $f(x) = e^x$ ist die natürliche Exponentialfunktion mit der eulerschen Zahl $e ≈ 2,718$. Ihre Besonderheit: Die Ableitung von $e^x$ ist wieder $e^x$! Das macht sie mathematisch sehr elegant.

Tangenten an e-Funktionen bestimmst du wie gewohnt: Steigung über die Ableitung, dann den y-Achsenabschnitt berechnen. Der natürliche Logarithmus ln ist die Umkehrfunktion zur e-Funktion: $e^{\ln(b)} = b$ und $\ln(e^c) = c$.

Jede Exponentialfunktion lässt sich als e-Funktion schreiben: $a^x = e^{\ln(a) \cdot x}$. Das ist praktisch für Ableitungen und Stammfunktionen.

Wichtig: $\log_a(b)$ ist die Zahl, mit der du a potenzieren musst, um b zu erhalten!

Analytische Geometrie

Punkte im 3D-Raum haben drei Koordinaten: A(3|1|2) liegt 3 Einheiten in x₁-, 1 Einheit in x₂- und 2 Einheiten in x₃-Richtung. Liegt eine Koordinate bei 0, befindet sich der Punkt auf einer der Koordinatenebenen.

Vektoren beschreiben Verschiebungen im Raum. Der Verbindungsvektor $\vec{AB}$ von Punkt A zu Punkt B berechnest du mit B - A. Der Ortsvektor verbindet den Ursprung mit einem Punkt, der Nullvektor hat keine Länge und keine Richtung.

Der Betrag eines Vektors $|\vec{v}| = \sqrt{v_1^2 + v_2^2 + v_3^2}$ gibt seine Länge an. Den Abstand zweier Punkte berechnest du als Betrag ihres Verbindungsvektors.

Diese Grundlagen brauchst du für Geraden, Ebenen und alle weiteren Berechnungen in der analytischen Geometrie.

Visualisierungstipp: Stelle dir Vektoren als Pfeile vor - das hilft beim räumlichen Verständnis!