Grundlagen der Ableitung

Die Potenzregel ist dein wichtigstes Tool: Aus $f(x) = ax^n$ wird $f'(x) = n \cdot ax^{n-1}$. Das funktioniert genauso bei Wurzeln und negativen Exponenten. Merke dir auch die Standardableitungen: $\sin(x) \rightarrow \cos(x)$, $\cos(x) \rightarrow -\sin(x)$, und Konstanten werden zu Null.

Die erste Ableitung $f'(x)$ zeigt dir die Steigung der Tangente an jeder Stelle. Ist $f'(x) > 0$, steigt die Funktion monoton. Bei $f'(x) < 0$ fällt sie, und bei $f'(x) = 0$ verläuft sie waagerecht.

Die zweite Ableitung $f''(x)$ beschreibt das Krümmungsverhalten. Positive Werte bedeuten Linkskrümmung (wie ein Lächeln), negative Werte Rechtskrümmung (wie ein trauriges Gesicht).

Tipp: Visualisiere dir immer, wie die Funktion aussieht - das macht die Ableitung viel verständlicher!

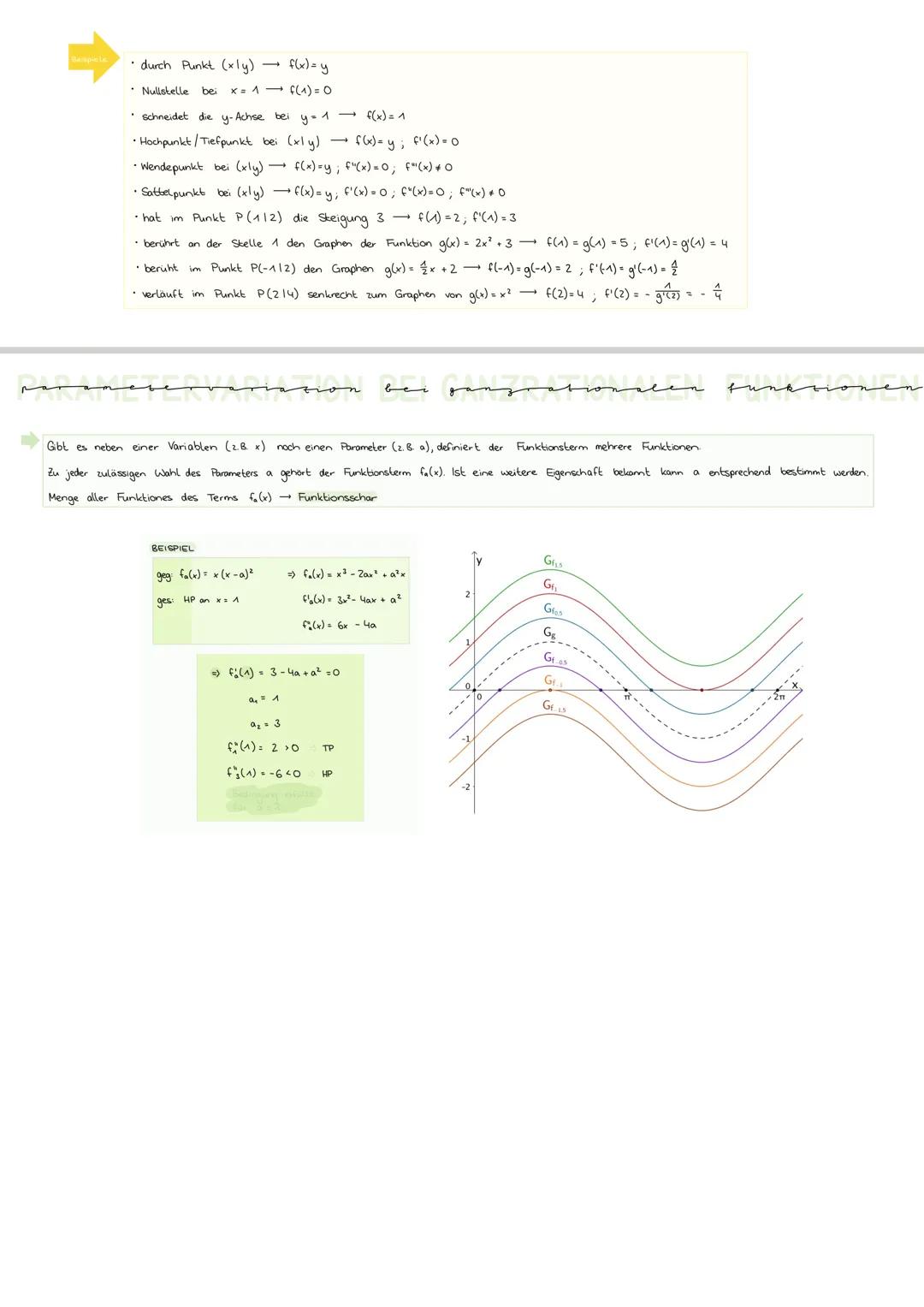
Bestimmen ganzrationaler Funktionen

Du gehst dabei systematisch vor: Erst skizzierst du grob den Verlauf, dann stellst du die allgemeine Funktionsgleichung mit Ableitungen auf. Anschließend formulierst du alle gegebenen Bedingungen und erstellst ein lineares Gleichungssystem (LGS).

Wichtige Regeln: Verwende immer den niedrigsten möglichen Grad und sorge dafür, dass du genauso viele Bedingungen wie Unbekannte hast. Bei punktsymmetrischen Funktionen mit ungeradem Grad fallen die geraden Exponenten weg.

Die Lösung des LGS gibt dir die gesuchte Funktion. Eine Probe mit dem CAS und ein Rückbezug zur ursprünglichen Situation runden deine Lösung ab.

Charakteristische Punkte bestimmen

Extrempunkte findest du über die notwendige Bedingung $f'(x) = 0$. Setze die x-Werte dann in $f(x)$ ein für die y-Koordinaten. Für die hinreichende Bedingung prüfst du das Vorzeichen von $f'(x)$: Wechsel von + zu - bedeutet Hochpunkt, von - zu + Tiefpunkt.

Wendepunkte erkennst du an $f''(x) = 0$. Hier ändert sich das Krümmungsverhalten der Funktion. Sattelpunkte sind spezielle Wendepunkte, die gleichzeitig die Extrempunkt-Bedingung erfüllen: $f'(x) = 0$ und $f''(x) \neq 0$.

Die Zusammenhänge zwischen $f(x)$, $f'(x)$ und $f''(x)$ sind dabei entscheidend: Wendepunkte von $f(x)$ sind Extrempunkte von $f'(x)$ und Nullstellen von $f''(x)$.

Bedingungen richtig formulieren

Verschiedene Situationen führen zu unterschiedlichen mathematischen Bedingungen. "Durch Punkt (x|y)" bedeutet einfach $f(x) = y$. Eine Nullstelle bei x = 1 schreibst du als $f(1) = 0$.

Für Extrempunkte brauchst du zwei Bedingungen: $f(x) = y$ für den Punkt und $f'(x) = 0$ für die waagerechte Tangente. Wendepunkte erkennst du an $f(x) = y$, $f''(x) = 0$ und $f'''(x) \neq 0$.

Berührungssituationen sind besonders: Wenn zwei Funktionen sich berühren, haben sie an der Stelle den gleichen Funktionswert UND die gleiche Steigung. Bei senkrechten Verläufen multiplizierst du die Steigungen - das Ergebnis muss -1 sein.

Merkhilfe: Berührung = gleicher Punkt + gleiche Steigung!

Parametervariationen bei Funktionsscharen

Eine Funktionsschar wie $f_a(x) = x \cdot (x-a)^2$ beschreibt unendlich viele Funktionen, je nach Wahl des Parameters a. Jeder a-Wert erzeugt eine andere Funktion der Schar.

Um spezielle Eigenschaften zu finden, leitest du wie gewohnt ab: $f'_a(x) = 3x^2 - 4ax + a^2$. Für Extrempunkte setzt du $f'_a(x) = 0$ und löst nach den entsprechenden Variablen auf.

Im Beispiel ergeben sich für verschiedene a-Werte unterschiedliche Extrempunkte. Die zweite Ableitung hilft dir zu entscheiden, ob es sich um Hoch- oder Tiefpunkte handelt. So verstehst du, wie sich die gesamte Funktionsschar verhält.