Normalverteilung vs. Binomialverteilung
Der große Unterschied liegt in diskret vs. stetig: Bei der Binomialverteilung zählst du einzelne Ereignisse (Münzwürfe, Personen), bei der Normalverteilung misst du kontinuierliche Werte (Größe, Gewicht, Zeit).
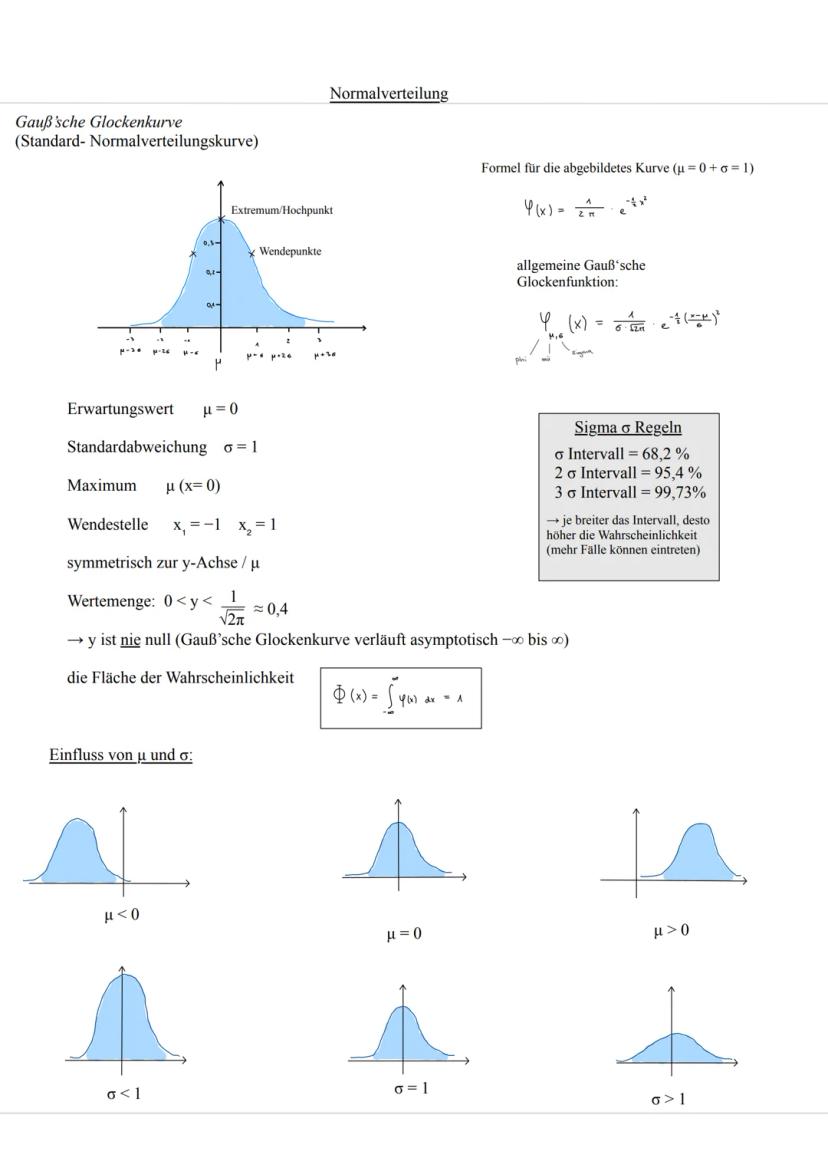
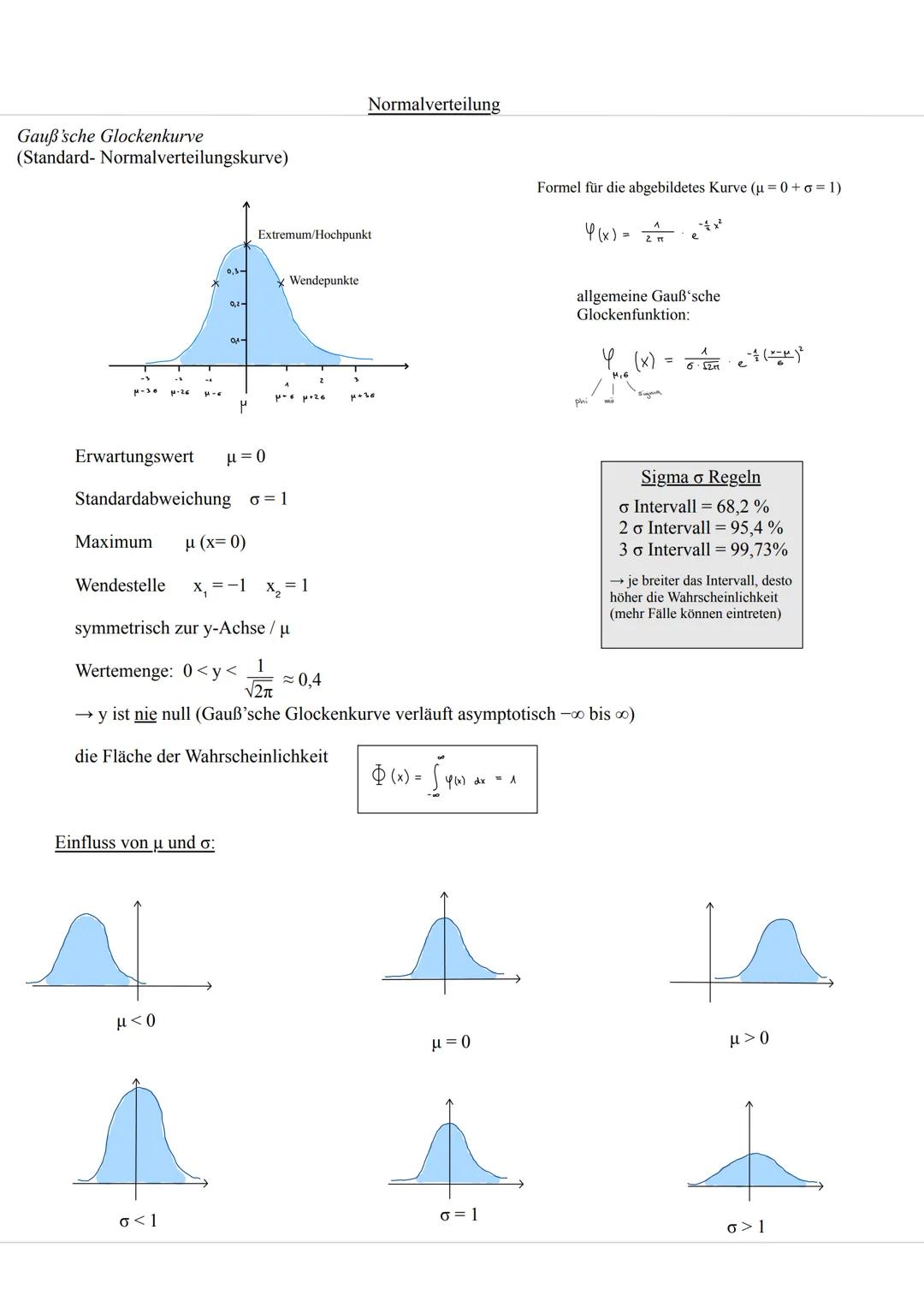
μ verschiebt die gesamte Kurve nach links oder rechts, während σ bestimmt, wie steil oder flach sie verläuft. Kleines σ = steile Kurve, großes σ = flache Kurve. Das ist wie bei einem Berg: schmaler Gipfel oder breiter Hügel.
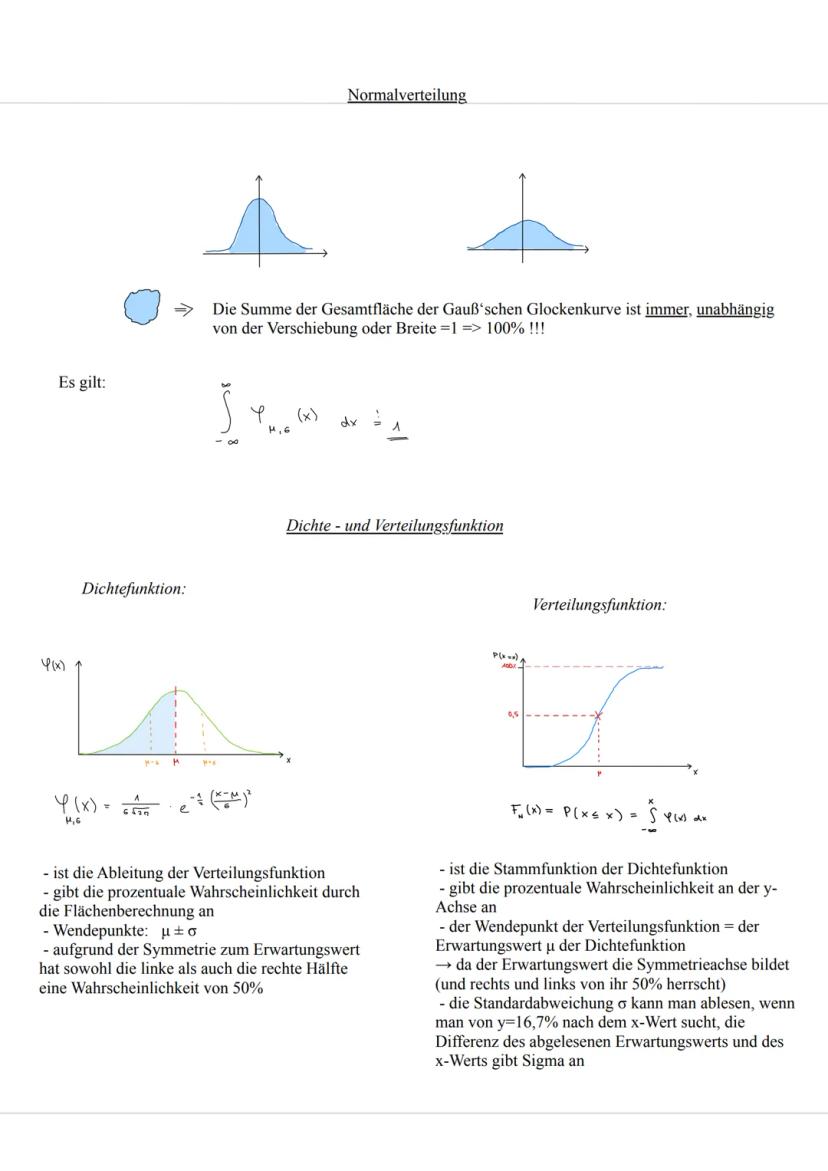
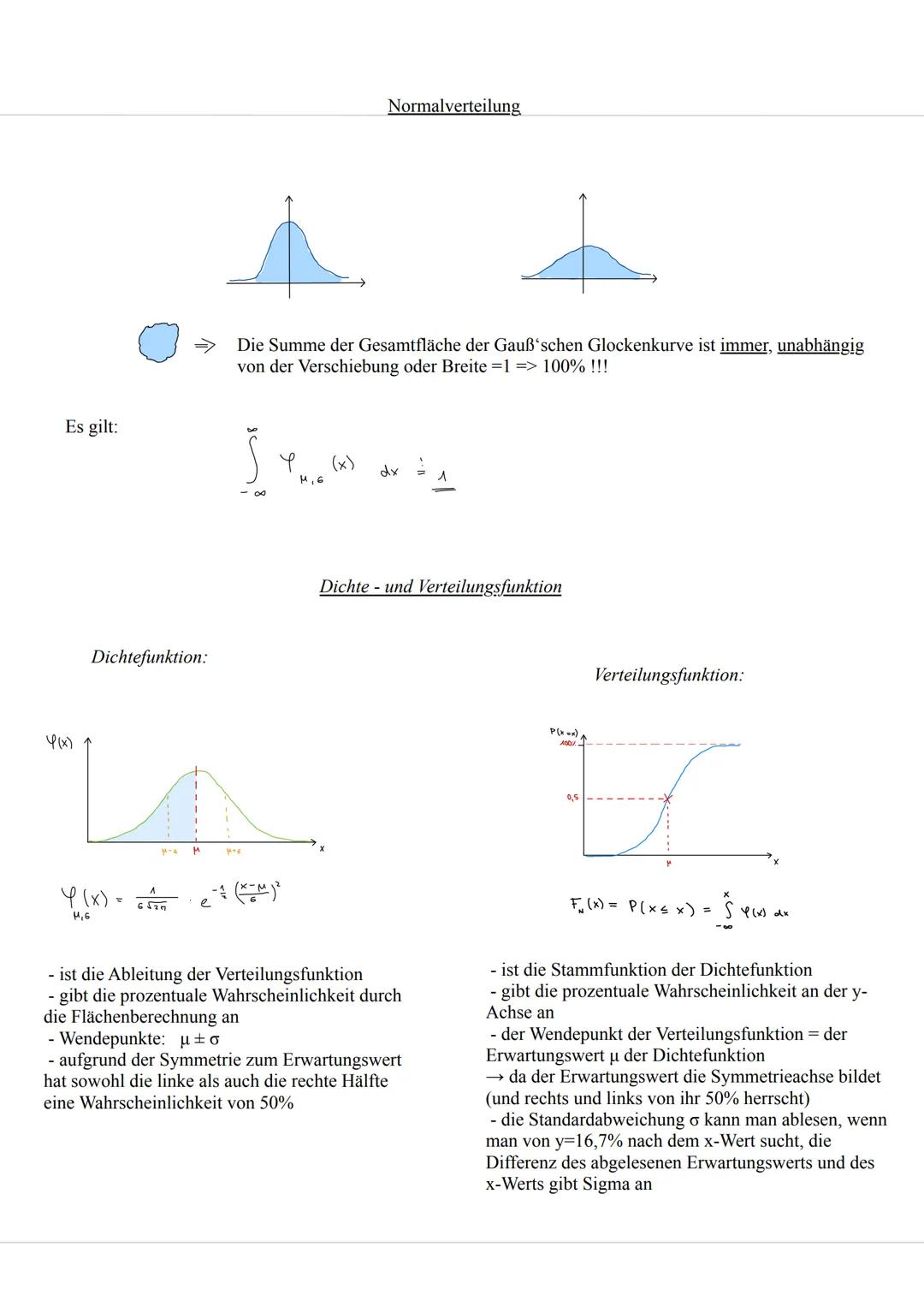
Bei stetigen Verteilungen gibt es keine Einzelwahrscheinlichkeiten - PX=2,5 ist immer 0! Du rechnest nur mit Intervallwahrscheinlichkeiten wie P(2 ≤ X ≤ 3).
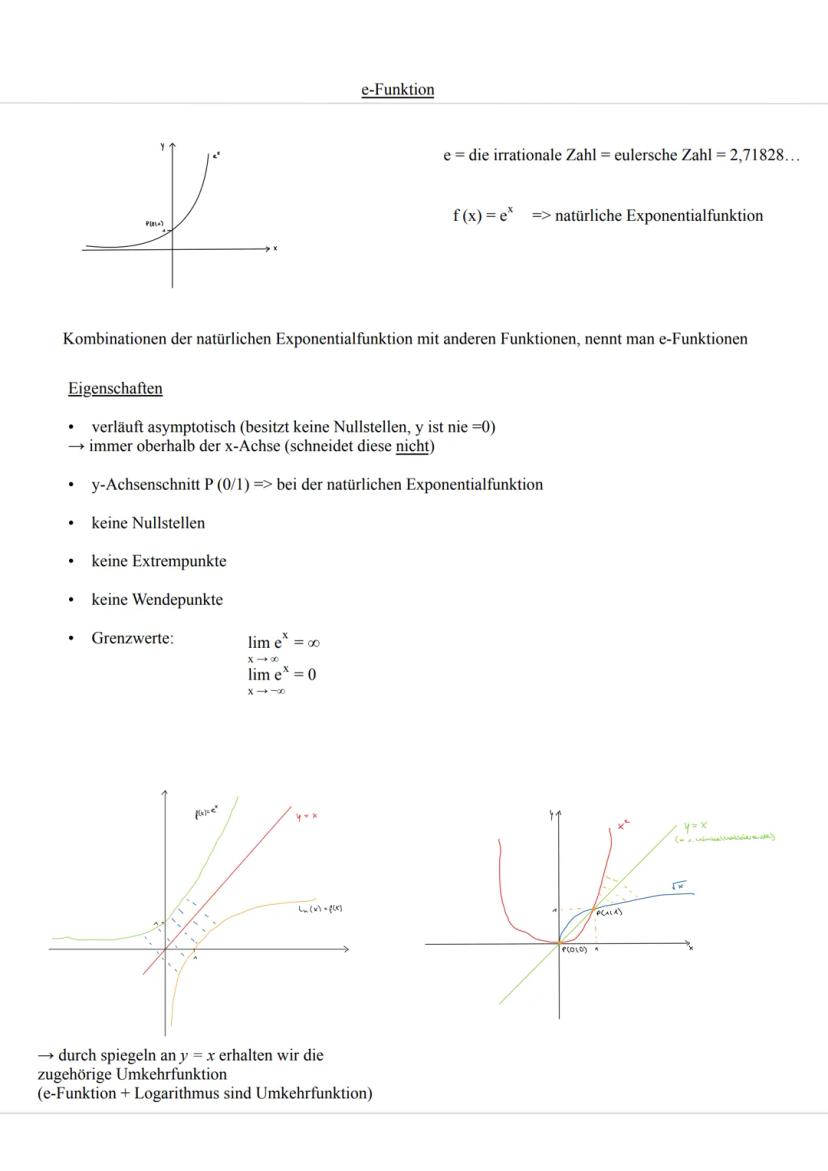
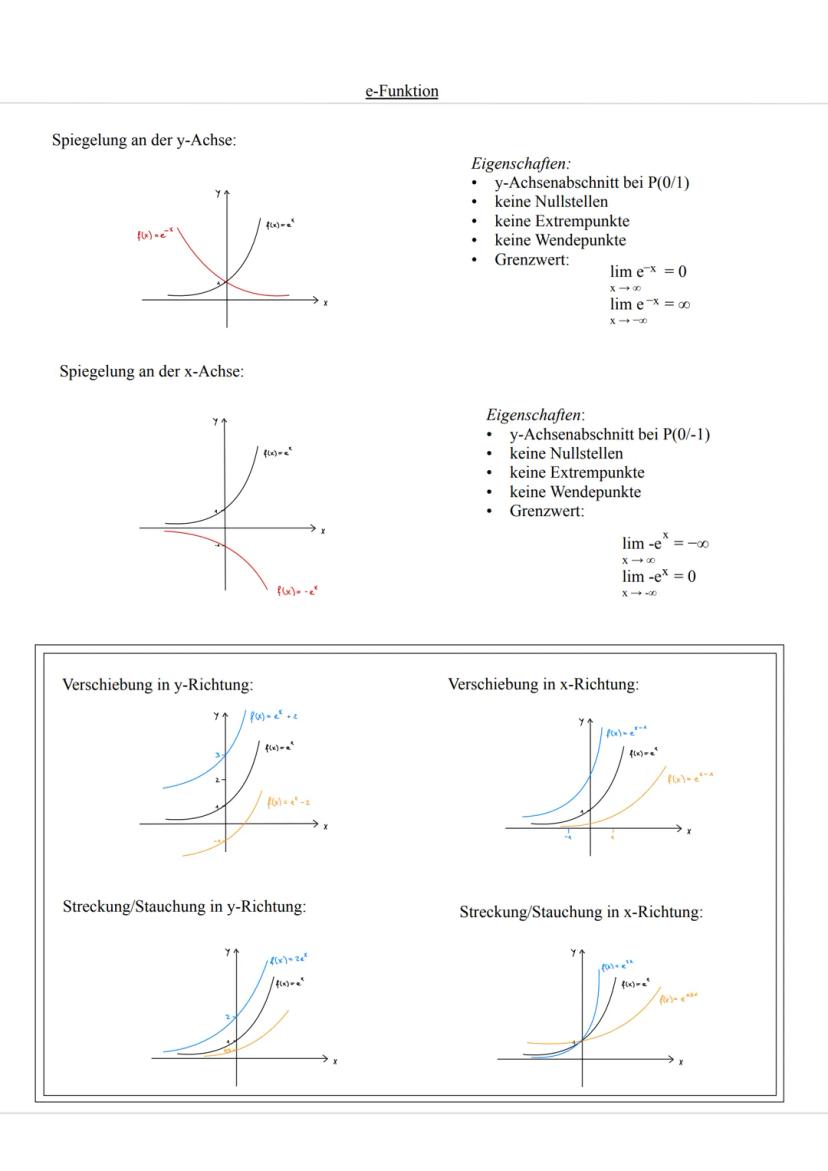
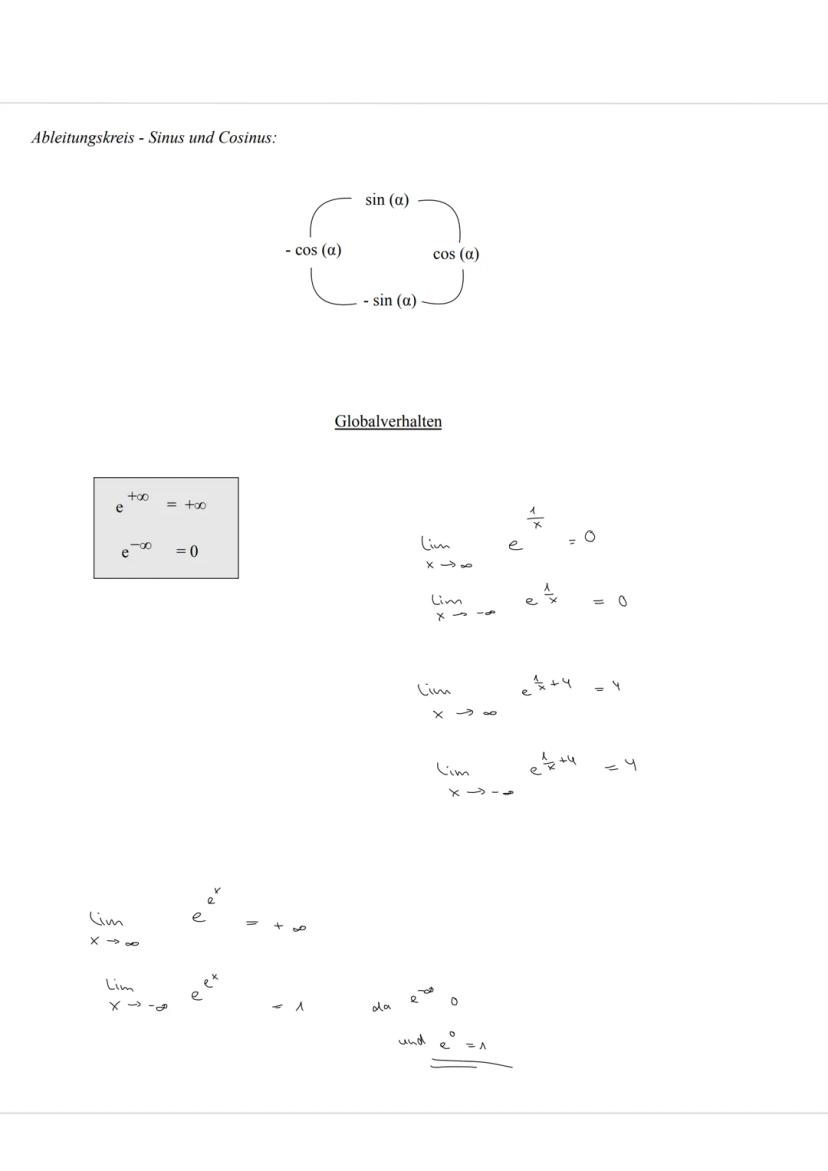
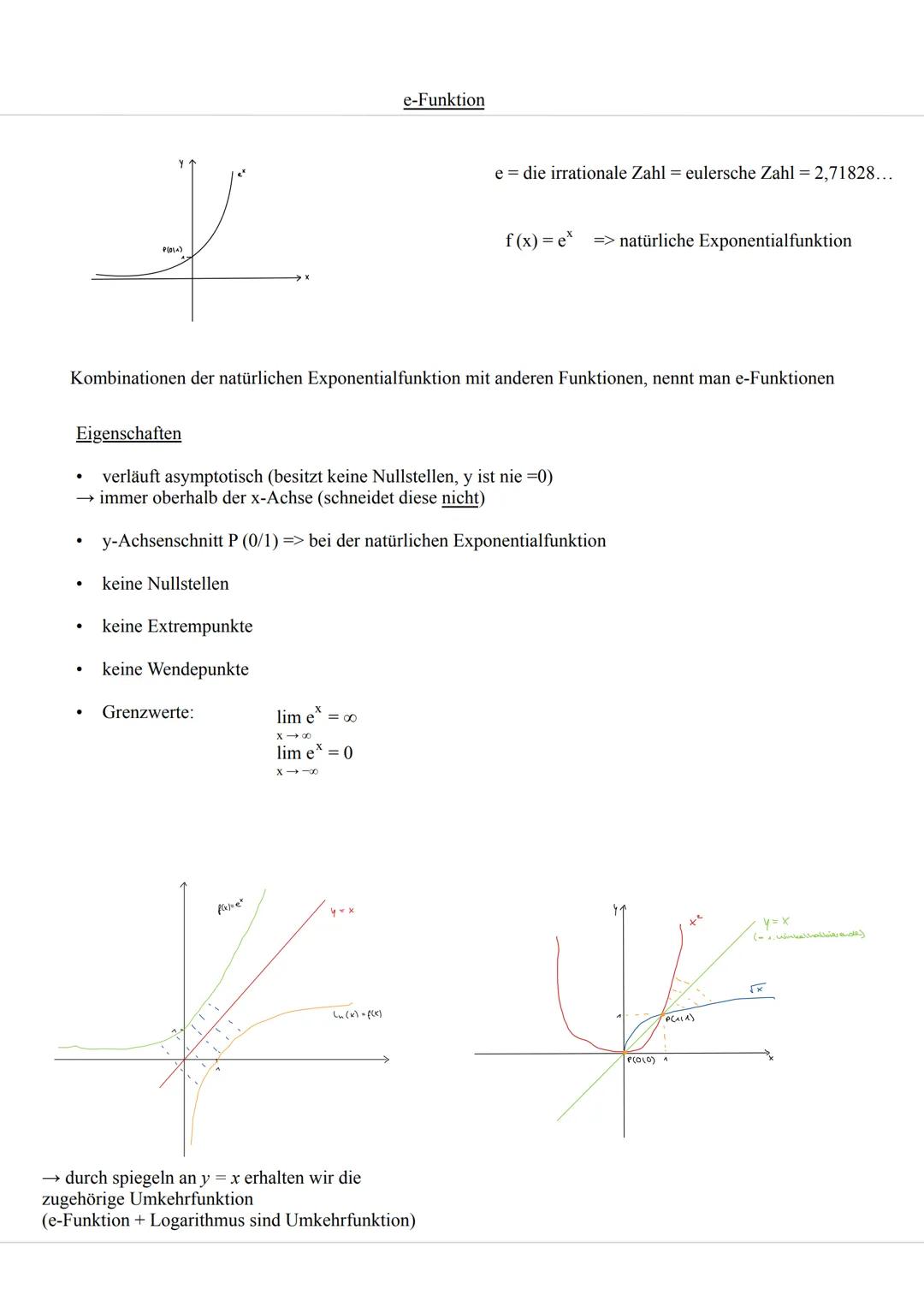
Praxistipp: Merke dir die e-Funktion ist immer positiv, deshalb sind alle y-Werte der Normalverteilung größer als null!