Mathematik

Graphen- und Figurentransformationen

Vertikale Streckung

3.850

•

7. Feb. 2026

•

4 Seiten

Quadratische Funktionen leicht erklärt – Klasse 9

Đana

@learnbydo

Quadratische Funktionen sind überall um dich herum – von der... Mehr anzeigen

1 / 4

# QUADRATISCHE
# FUNKTIONIN
Normalform
$f(x)=ax² + bx + c$
Scheitelpunktform: $f(x)=a(x-d)²+e$ S (d/e)

Der Graph einer quatratischen Funkti

Grundlagen quadratischer Funktionen

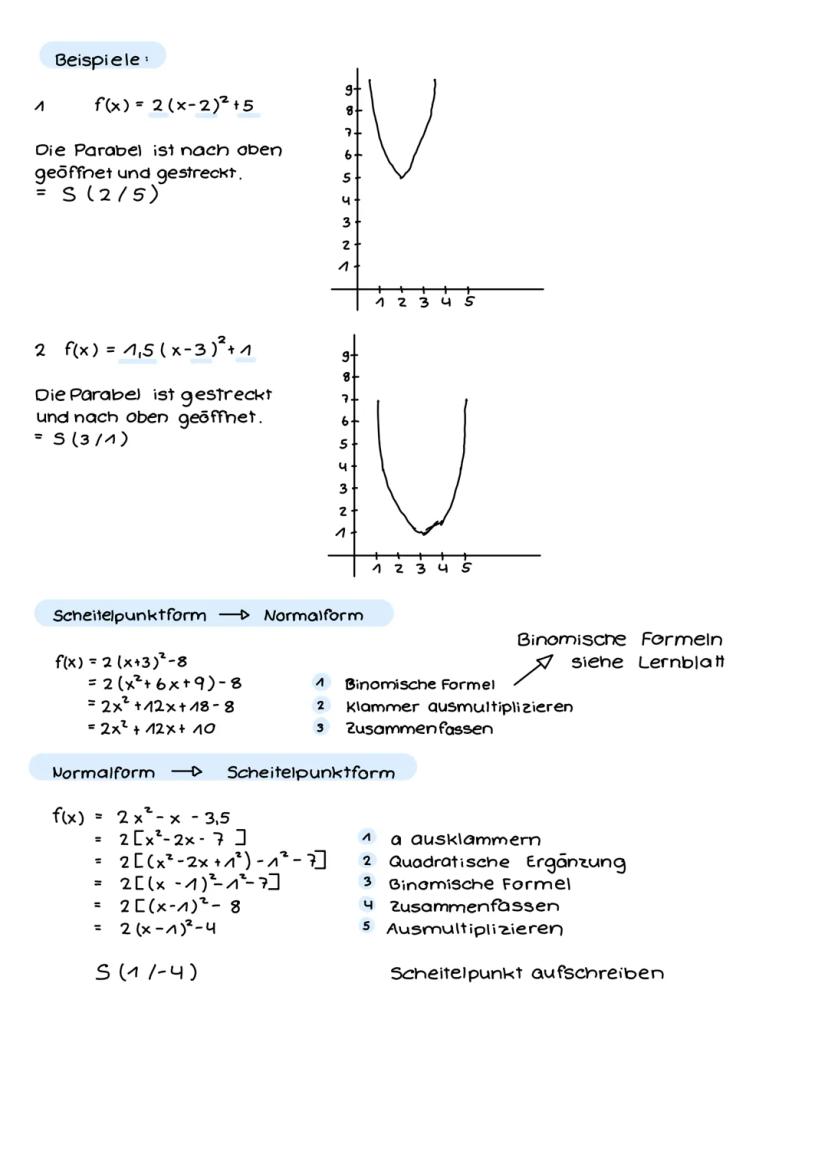
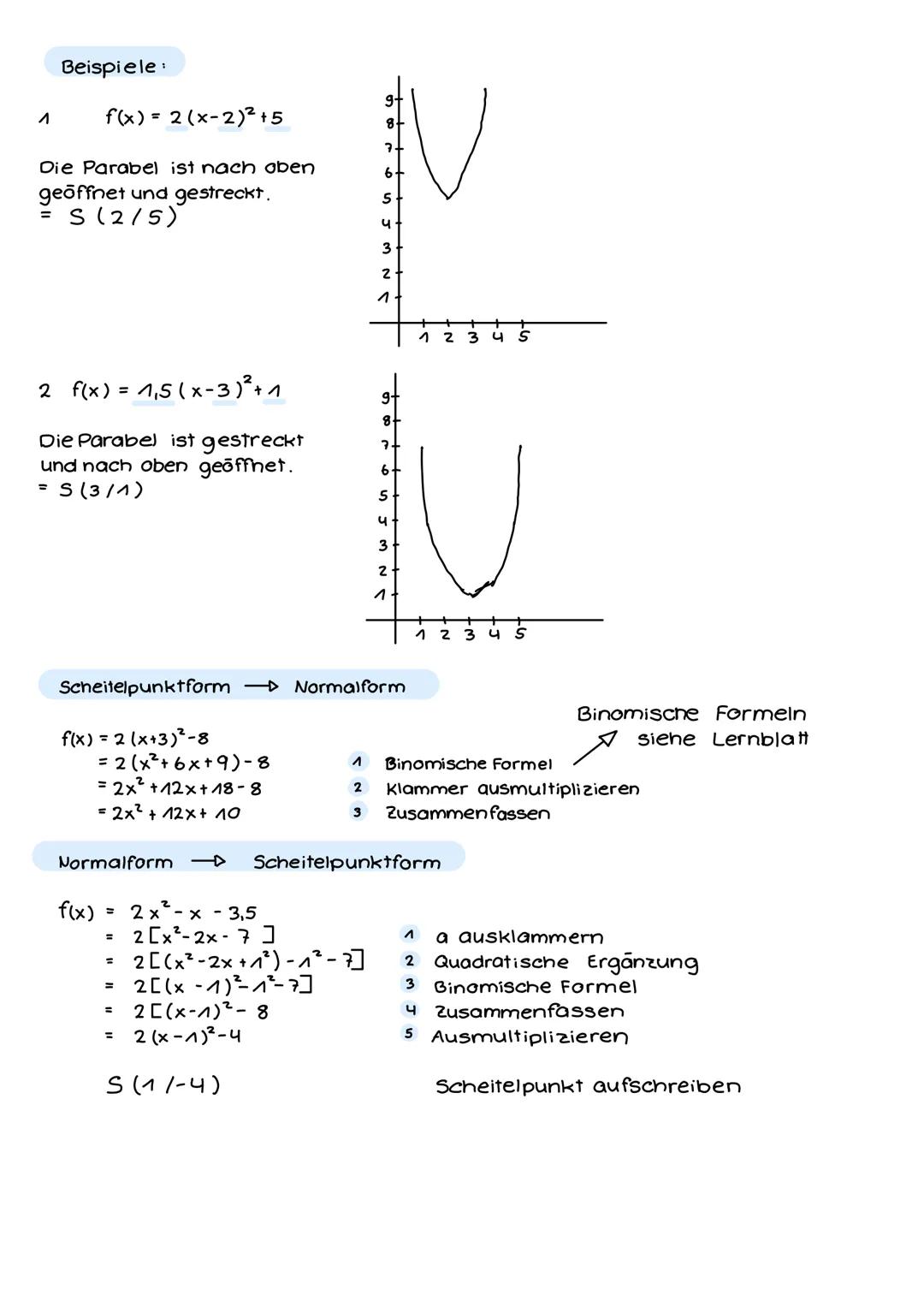
Quadratische Funktionen haben zwei wichtige Darstellungsformen: die Normalform f(x) = ax² + bx + c und die Scheitelpunktform f(x) = a $x - d$ ² + e. Die Scheitelpunktform ist dein bester Freund beim Zeichnen, weil du sofort siehst, wo der Scheitelpunkt S $d/e$ liegt.

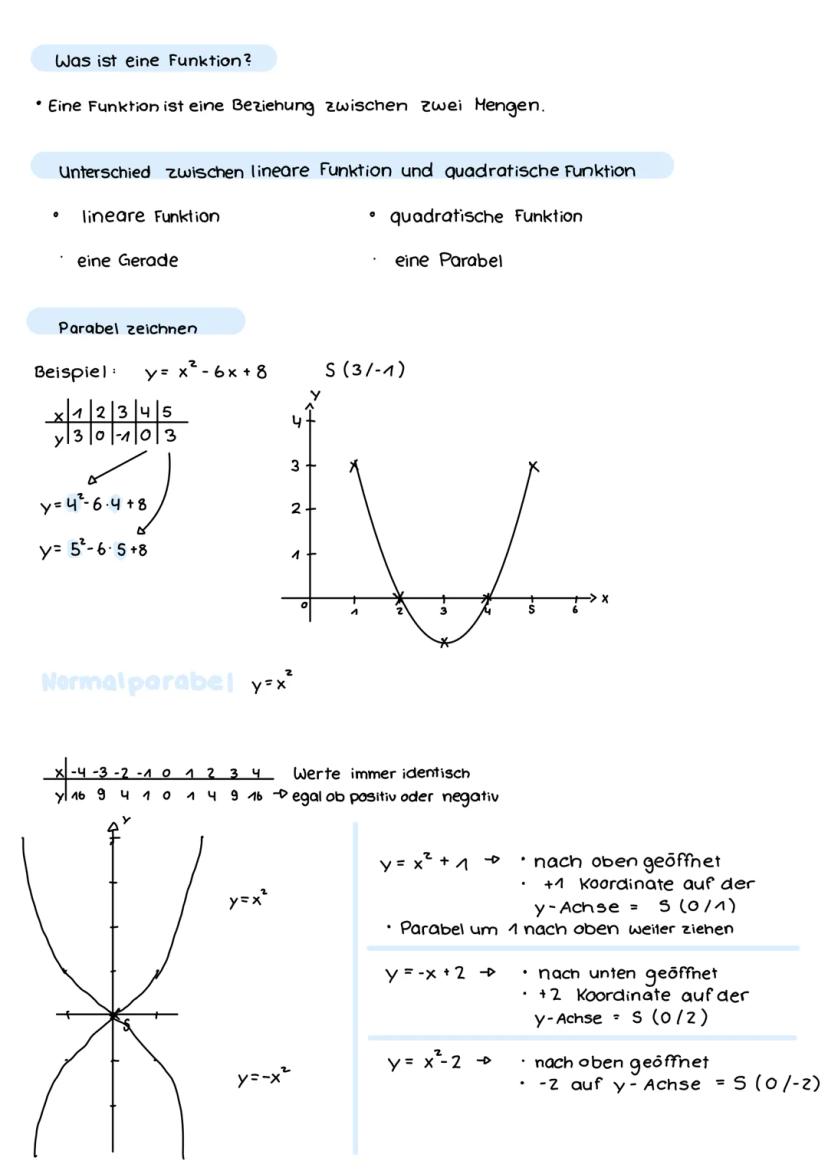
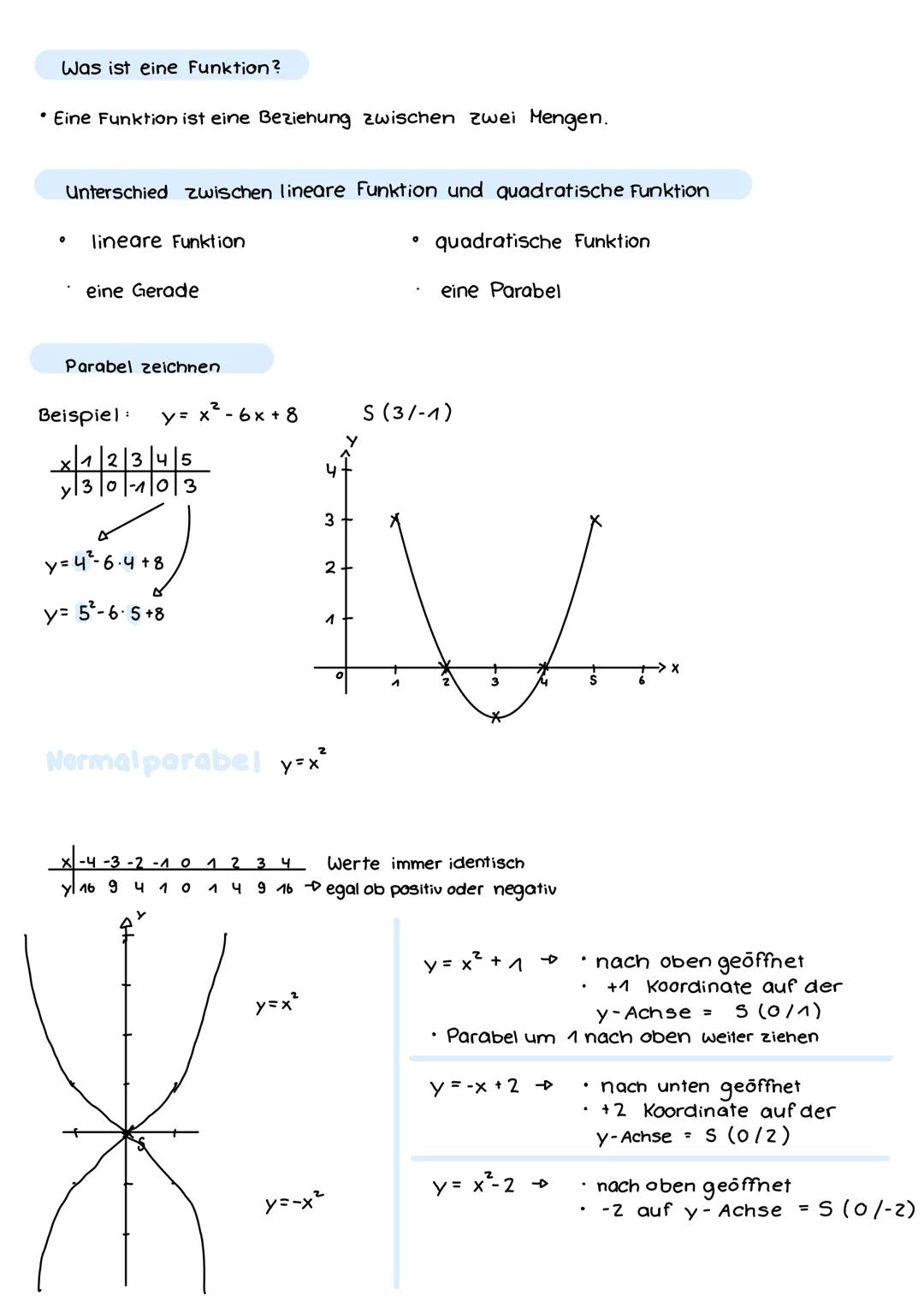
Der Parameter a verrät dir alles über die Form deiner Parabel. Ist a > 0, öffnet sich die Parabel nach oben wie ein U. Ist a < 0, öffnet sie sich nach unten wie ein umgedrehtes U. Je größer |a|, desto schmaler wird die Parabel – je kleiner |a|, desto breiter.

Merktrick: Bei der Verschiebung an der x-Achse denkst du umgekehrt! f(x) = $x - 3$ ² verschiebt nach rechts zu x = 3, während f(x) = $x + 2$ ² nach links zu x = -2 verschiebt.

💡 Tipp: Die Scheitelpunktform zeigt dir auf einen Blick, wo deine Parabel liegt und wie sie aussieht – nutze sie zum Zeichnen!

Umrechnung zwischen den Formen

Manchmal brauchst du die Normalform, manchmal die Scheitelpunktform – zum Glück kannst du easy zwischen beiden wechseln. Von Scheitelpunkt- zur Normalform multiplizierst du einfach die binomischen Formeln aus und fasst zusammen.

Der Weg zurück ist etwas kniffliger: Du klammerst zuerst den Faktor a aus und machst dann die quadratische Ergänzung. Das bedeutet, du ergänzt geschickt ein Quadrat, damit du die binomische Formel rückwärts anwenden kannst.

Beispiel-Schritt für Schritt: Bei f(x) = 2x² - 4x - 1,5 klammerst du erst 2 aus: 2 $x² - 2x - 0,75$ . Dann ergänzt du $x - 1$ ² und gleichst mit -1 aus.

💡 Tipp: Die quadratische Ergänzung ist wie ein Puzzle – du fügst ein passendes Stück hinzu und nimmst es gleichzeitig wieder weg!

Parabeln zeichnen und verstehen

Eine Parabel unterscheidet sich grundlegend von einer Geraden: Während lineare Funktionen immer gleich steigen oder fallen, werden quadratische Funktionen immer steiler oder flacher. Die Normalparabel y = x² ist dein Ausgangspunkt für alle anderen Parabeln.

Beim Zeichnen startest du am besten mit einer Wertetabelle um den Scheitelpunkt herum. Die Parabel ist achsensymmetrisch zur Scheitelpunkt-Senkrechten, das heißt, links und rechts vom Scheitelpunkt sind die y-Werte in gleichem Abstand identisch.

Verschiebungen erkennst du sofort: y = x² + 3 verschiebt die Normalparabel um 3 nach oben, y = x² - 2 um 2 nach unten. Der Scheitelpunkt wandert entsprechend mit.

💡 Tipp: Nutze die Symmetrie! Wenn du den Punkt (1/3) hast, kennst du automatisch auch den Punkt (-1/3) auf der anderen Seite.

Streckung und Stauchung von Parabeln

Der Faktor vor x² bestimmt, wie breit oder schmal deine Parabel wird. Ist dieser Faktor größer als 1, wird die Parabel schmaler (gestreckt). Ist er zwischen 0 und 1, wird sie breiter (gestaucht).

Konkrete Beispiele: y = 2x² ist schmaler als die Normalparabel, y = 0,5x² ist breiter. Bei negativen Faktoren wie y = -2x² hast du zusätzlich eine Spiegelung an der x-Achse – die Parabel öffnet nach unten.

Kombinierte Verschiebungen wie y = - $x + 2$ ² + 1 kannst du Schritt für Schritt analysieren: Scheitelpunkt bei (-2/1), nach unten geöffnet, normale Breite. So behältst du bei komplexeren Funktionen den Überblick.

💡 Tipp: Zeichne zuerst die Grundform, dann verschiebe sie – das ist viel einfacher als alles auf einmal zu machen!

Wir dachten schon, du fragst nie...

Was ist der Knowunity KI-Begleiter?

Unser KI-Begleiter ist ein speziell für Schüler entwickeltes KI-Tool, das mehr als nur Antworten bietet. Basierend auf Millionen von Knowunity-Inhalten liefert er relevante Informationen, personalisierte Lernpläne, Quizze und Inhalte direkt im Chat und passt sich deinem individuellen Lernweg an.

Wo kann ich die Knowunity-App herunterladen?

Du kannst die App im Google Play Store und im Apple App Store herunterladen.

Ist Knowunity wirklich kostenlos?

Genau! Genieße kostenlosen Zugang zu Lerninhalten, vernetze dich mit anderen Schülern und hol dir sofortige Hilfe – alles direkt auf deinem Handy.

Beliebtester Inhalt: Vertikale Streckung

Graphentransformationen verstehen

Erfahren Sie alles über die Verschiebung und Streckung von Graphen. Diese Zusammenfassung behandelt die Grundlagen der Transformationen von Funktionen, einschließlich horizontaler und vertikaler Verschiebungen sowie Streckungen in x- und y-Richtung. Ideal für Studierende, die sich auf Prüfungen vorbereiten oder ihr Verständnis von Graphen vertiefen möchten.