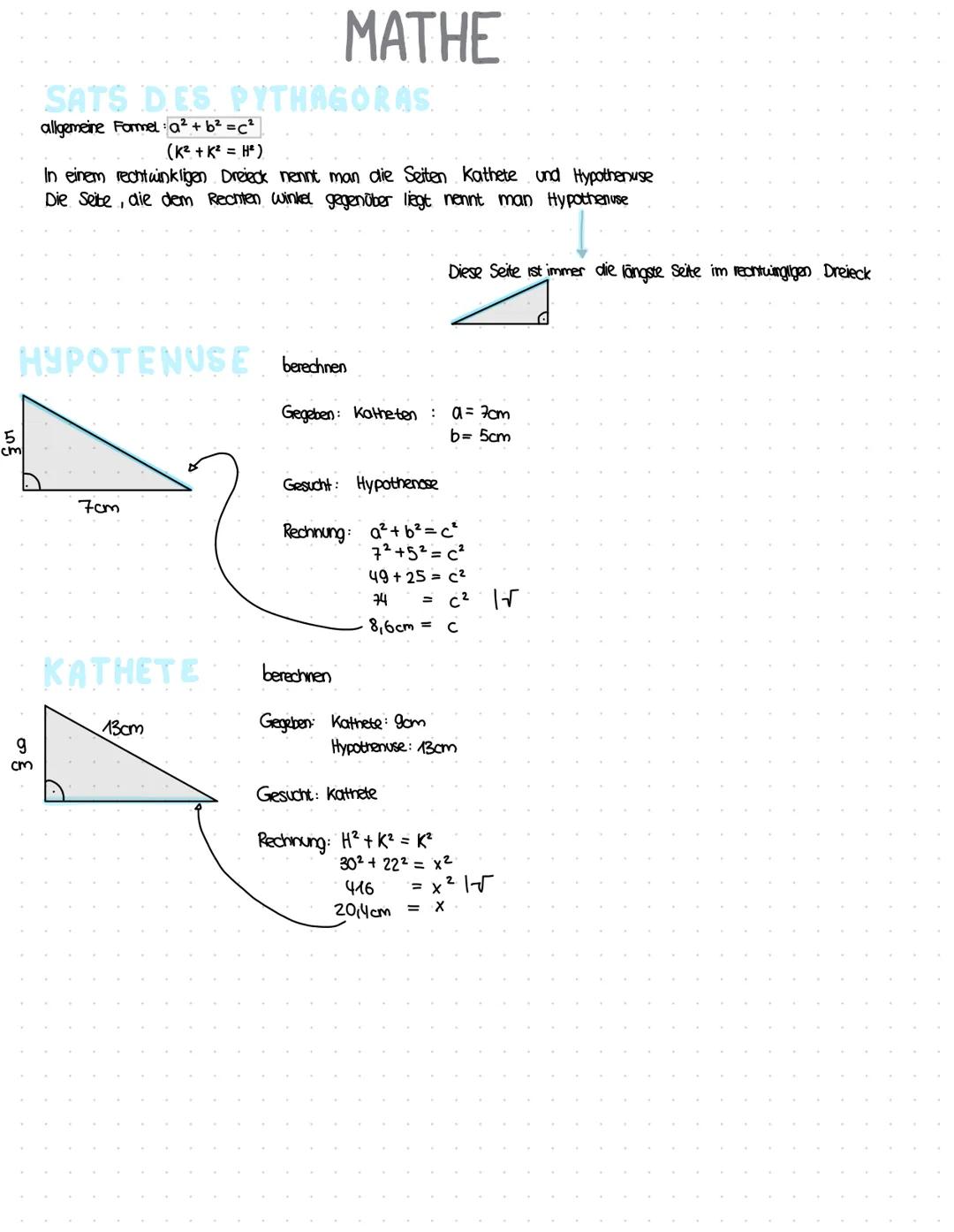
Satz des Pythagoras

In einem rechtwinkligen Dreieck gibt es drei Seiten: zwei Katheten und eine Hypotenuse. Die Hypotenuse liegt dem rechten Winkel gegenüber und ist immer die längste Seite des Dreiecks.

Der Satz des Pythagoras beschreibt die Beziehung zwischen diesen Seiten mit der Formel: a² + b² = c². Dabei sind a und b die Längen der Katheten und c ist die Länge der Hypotenuse. Man kann diese Formel auch als K² + K² = H² schreiben.

Mit dieser Formel kannst du eine unbekannte Seite berechnen, wenn du die anderen beiden kennst. Möchtest du zum Beispiel die Hypotenuse berechnen, setzt du die bekannten Katheten ein: Bei a = 7cm und b = 5cm lautet die Rechnung 7² + 5² = c², also 49 + 25 = 74 = c². Die Hypotenuse ist somit √74 ≈ 8,6cm lang.

💡 Merkhilfe: Denk daran, dass die Hypotenuse immer die längste Seite ist und dem rechten Winkel gegenüberliegt. Die Katheten bilden den rechten Winkel.

Soll eine Kathete berechnet werden, stellst du die Formel einfach um. Bei bekannter Hypotenuse c und einer Kathete a lautet die Formel für die andere Kathete: b² = c² - a². Zum Beispiel: Mit einer Hypotenuse von 13cm und einer Kathete von 9cm berechnest du b² = 13² - 9² = 169 - 81 = 88, also b ≈ 9,4cm.