Sinus, Kosinus, Tangens - Die Grundlagen
Stell dir vor, du stehst vor einem Dreieck und willst wissen, wie groß ein Winkel oder eine Seite ist. Genau dafür brauchst du die trigonometrischen Funktionen! Sie funktionieren wie Werkzeuge, mit denen du rechtwinklige Dreiecke "knacken" kannst.
Sinus ist das Verhältnis von Gegenkathete zur Hypotenuse: sin(α) = Gegenkathete/Hypotenuse. Die Gegenkathete liegt dem Winkel gegenüber, die Ankathete grenzt an den Winkel an.
Kosinus zeigt das Verhältnis von Ankathete zur Hypotenuse: cos(α) = Ankathete/Hypotenuse. Tangens verbindet beide Katheten: tan(α) = Gegenkathete/Ankathete.
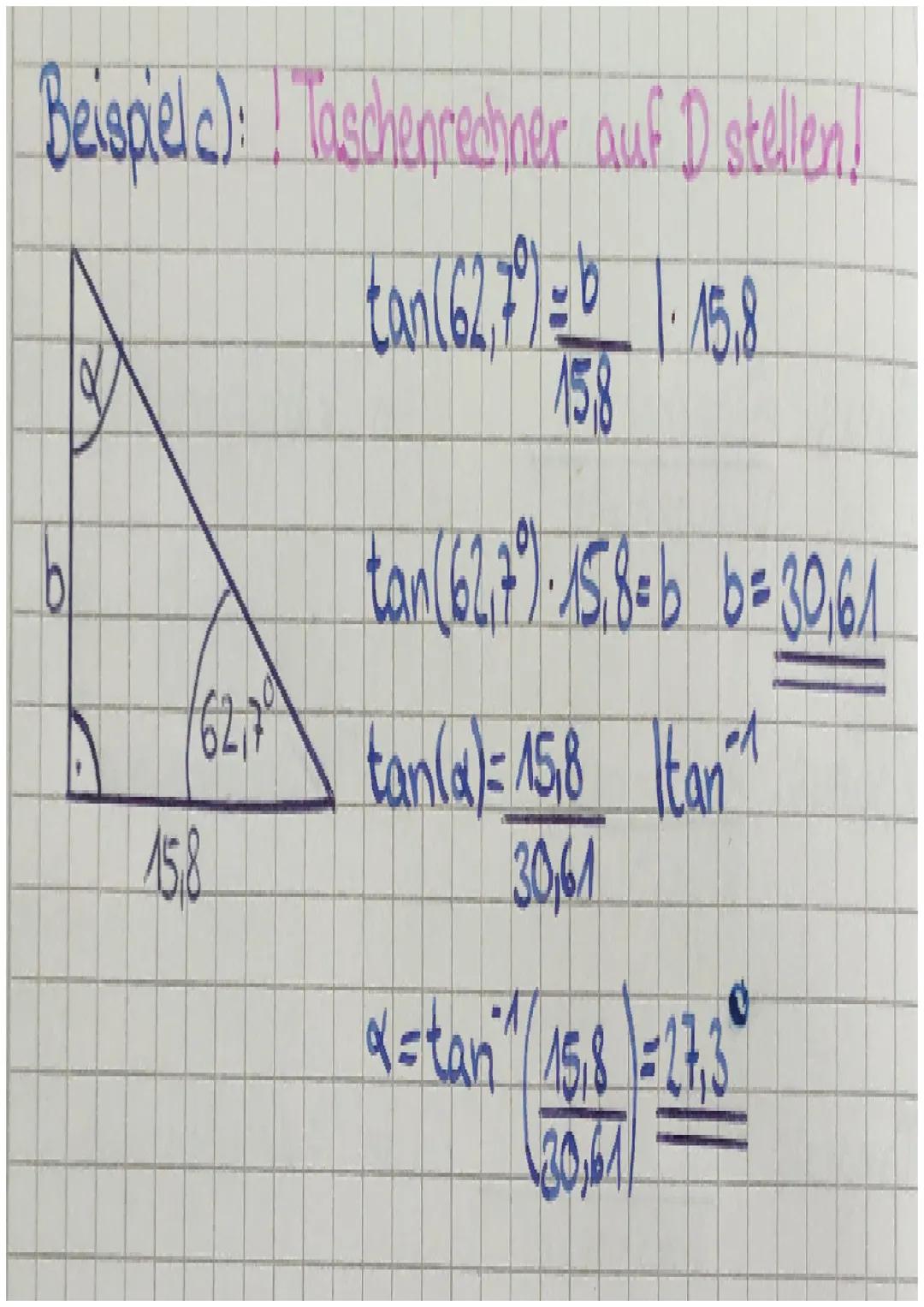
Wichtig: Stelle deinen Taschenrechner immer auf "D" für Grad, sonst bekommst du falsche Ergebnisse!
Im Beispiel mit der Hypotenuse 24,9 und der Gegenkathete 12,7 berechnest du: α = sin⁻¹(12,7/24,9) = 30,67°. Den zweiten Winkel findest du durch: β = 180° - 30,67° - 90° = 59,33°.