Trigonometrische Funktionen

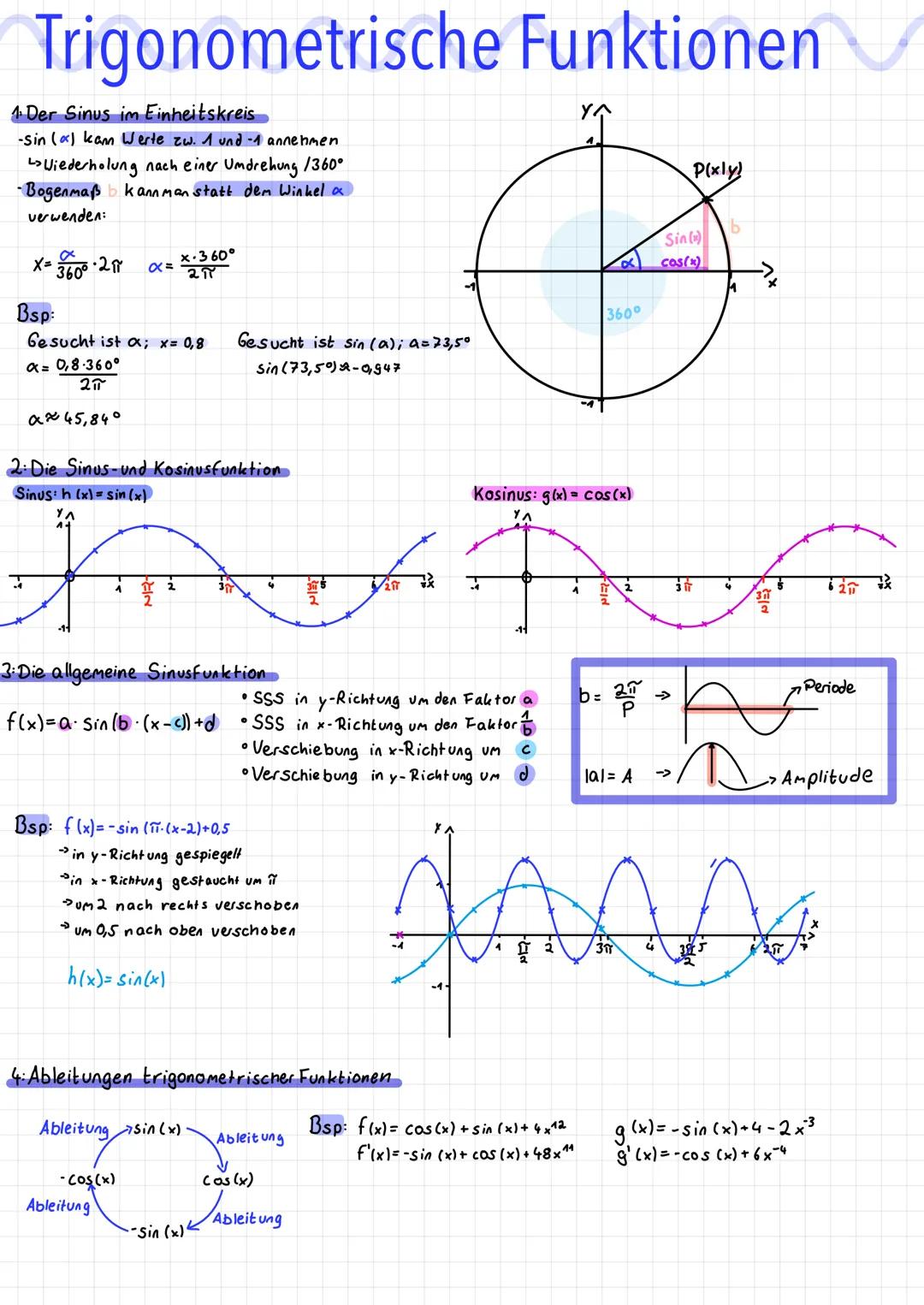
Der Sinus im Einheitskreis ist dein Startpunkt für alle trigonometrischen Funktionen. Sin$a$ kann nur Werte zwischen 1 und -1 annehmen - das ist seine natürliche Grenze. Nach einer vollständigen Umdrehung (360°) wiederholt sich alles wieder.

Statt mit Grad-Winkeln kannst du auch mit dem Bogenmaß arbeiten. Die Umrechnung funktioniert so: x = $α/360$ · 2π oder umgekehrt α = (x · 360°)/(2π). Das Bogenmaß macht viele Rechnungen später einfacher.

Die Grundfunktionen Sinus h$x$ = sin$x$ und Kosinus g$x$ = cos$x$ sind die Basis für alle weiteren trigonometrischen Berechnungen. Sie schwingen beide wellenförmig zwischen -1 und 1.

Bei der allgemeinen Sinusfunktion f$x$ = a·sin$b·(x-c)$+d passiert richtig viel: Der Parameter |a| bestimmt die Amplitude (Schwingungsweite), b = 2π/P gibt die Periode vor, c verschiebt horizontal und d vertikal. Negative a-Werte spiegeln die Funktion an der x-Achse.

Merktipp: Die Ableitung von sin$x$ ist cos$x$, die von cos$x$ ist -sin$x$. Das wechselt immer schön im Kreis!