Die Wurzelfunktion - Grundlagen und Eigenschaften
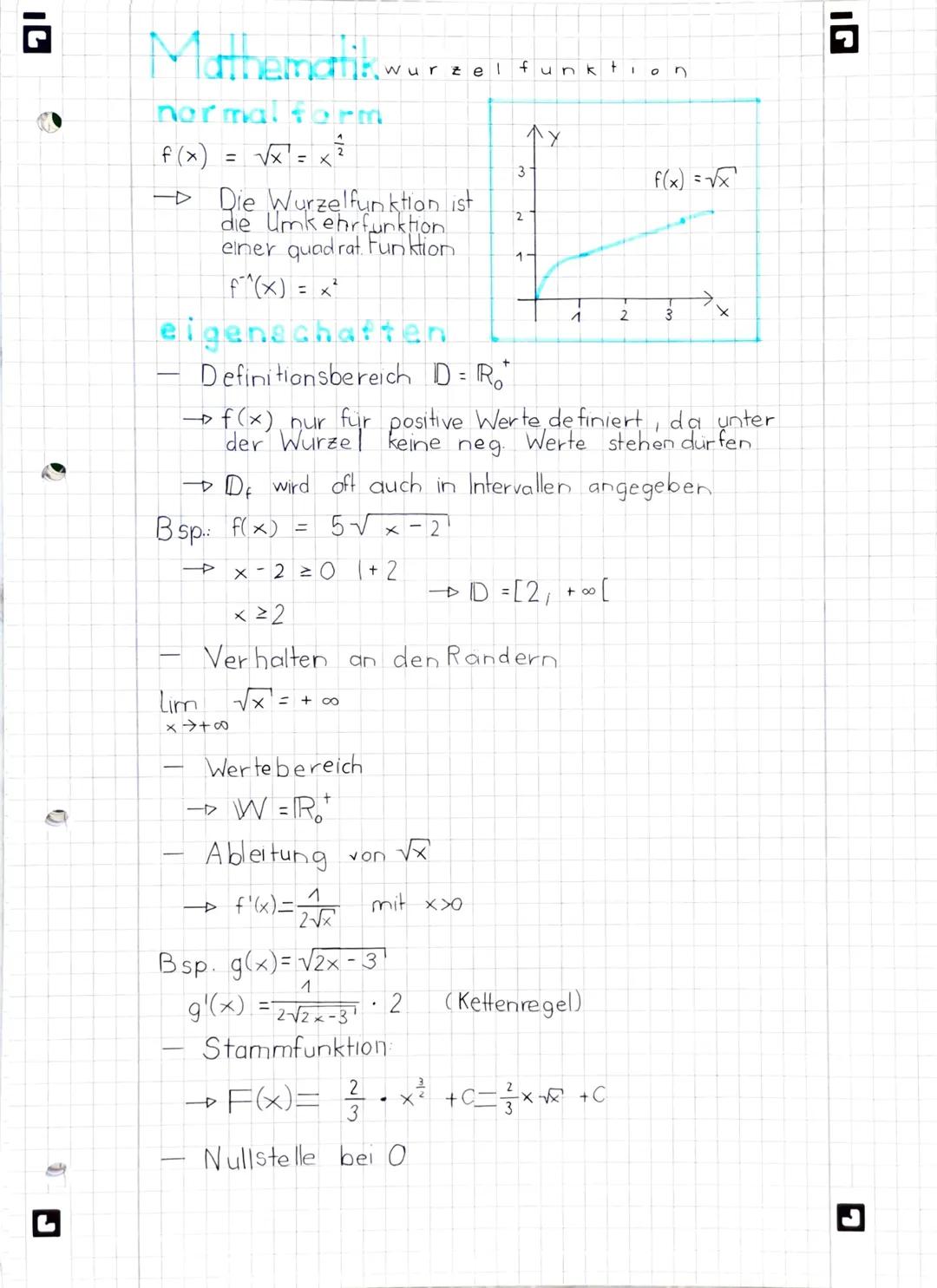
Die Wurzelfunktion f(x) = √x ist nichts anderes als die Umkehrfunktion der Quadratfunktion f(x) = x². Das bedeutet, sie "macht rückgängig", was das Quadrieren bewirkt hat.
Der wichtigste Punkt: Die Funktion ist nur für positive Werte definiert, weil du aus negativen Zahlen keine reelle Wurzel ziehen kannst. Deshalb ist der Definitionsbereich D = ℝ₀⁺, also alle Zahlen ab null aufwärts.
Bei verschobenen Wurzelfunktionen wie f(x) = 5√x−2 musst du aufpassen: Hier muss x-2 ≥ 0 sein, also x ≥ 2. Der Definitionsbereich ist dann [2, +∞[.
Merktipp: Der Ausdruck unter der Wurzel muss immer ≥ 0 sein!
Die Funktion startet bei null und wächst ins Unendliche, wird aber immer flacher. Deshalb ist auch der Wertebereich W = ℝ₀⁺.