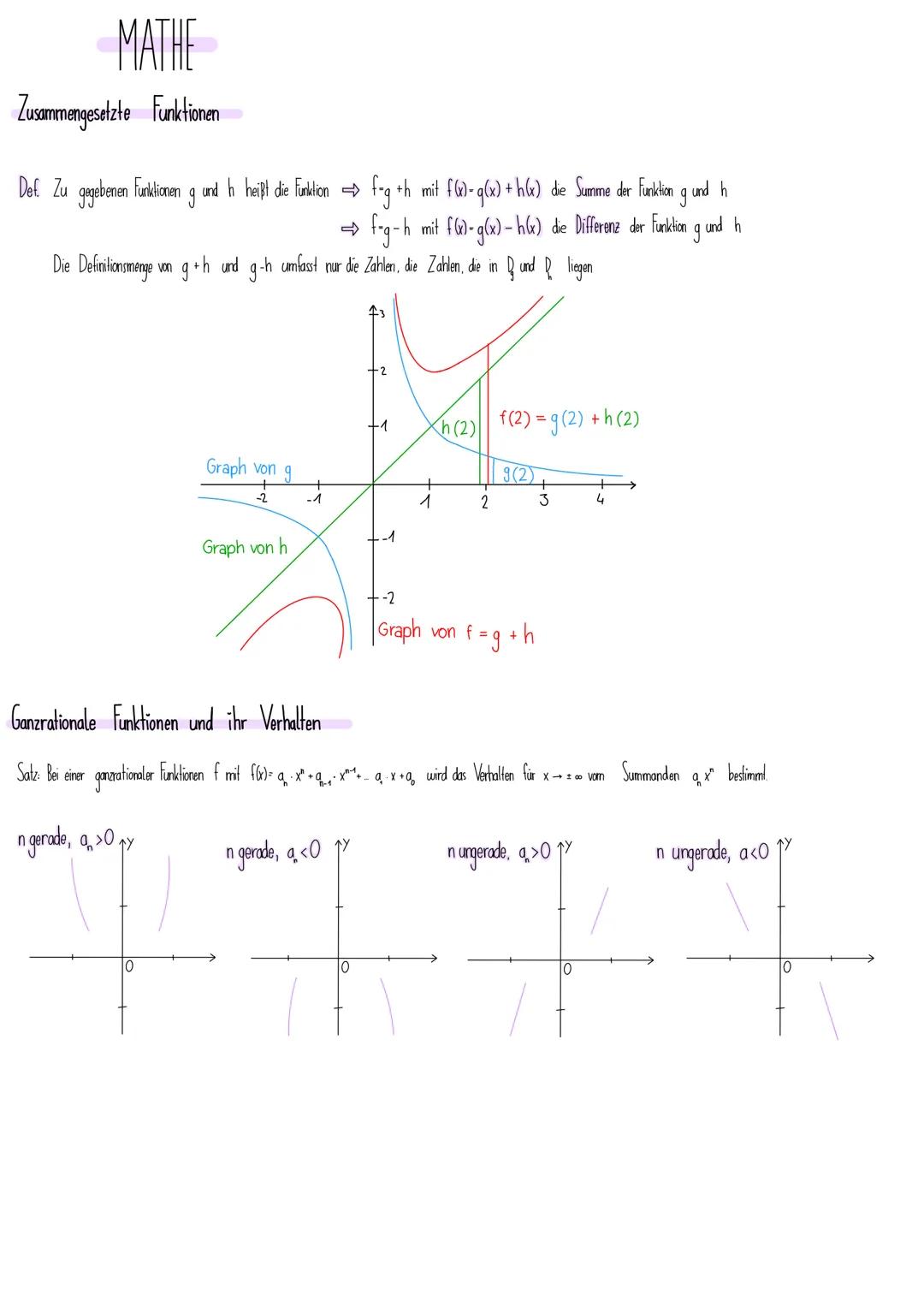
Zusammengesetzte Funktionen

Du kannst Funktionen genauso wie normale Zahlen addieren und subtrahieren! Wenn du zwei Funktionen g und h hast, entsteht durch f = g + h eine neue Funktion, bei der du einfach die y-Werte addierst: f$x$ = g$x$ + h$x$.

Bei der Definitionsmenge musst du aufpassen: Die neue Funktion f existiert nur dort, wo beide ursprünglichen Funktionen g und h definiert sind. Das ist wie bei einer Schnittmenge - nur die x-Werte, die in beiden Definitionsmengen liegen, sind erlaubt.

Grafisch bedeutet das: Um den Graphen von f = g + h zu zeichnen, addierst du für jeden x-Wert die entsprechenden y-Werte der beiden Graphen. Das Beispiel zeigt dir, wie bei x = 2 die y-Werte von g und h zusammengezählt werden.

Merktipp: Bei zusammengesetzten Funktionen immer zuerst die Definitionsmenge bestimmen, dann punktweise die Funktionswerte berechnen!

Verhalten ganzrationaler Funktionen

Das Verhalten für x → ∞ bei ganzrationalen Funktionen ist eigentlich ganz einfach zu bestimmen. Du musst nur auf den höchsten Summanden schauen - alle anderen werden bei sehr großen x-Werten unwichtig.

Wenn deine Funktion f$x$ = aₙxⁿ + ... + a₁x + a₀ ist, dann entscheidet nur aₙxⁿ über das Verhalten. Dabei gibt es vier einfache Regeln: Bei geradem n und positivem a geht der Graph nach oben, bei negativem a nach unten.

Bei ungeradem n und positivem a steigt der Graph von links unten nach rechts oben, bei negativem a genau umgekehrt. Diese Muster helfen dir, das Verhalten jeder ganzrationalen Funktion sofort zu erkennen.