Punkte und Vektoren im Raum

Stell dir vor, du willst jemandem erklären, wo sich ein Objekt in deinem Zimmer befindet - genau das machen wir hier mathematisch! Im dreidimensionalen Raum brauchst du drei Koordinaten (x₁, x₂, x₃), um einen Punkt P eindeutig zu bestimmen.

Den Abstand zwischen zwei Punkten berechnest du mit einer erweiterten Version des Satzes von Pythagoras: |AB| = √$(b₁-a₁)² + (b₂-a₂)² + (b₃-a₃)²$. Das ist im Grunde zweimal hintereinander Pythagoras anwenden.

Vektoren sind wie Wegbeschreibungen - sie zeigen dir, wie du von einem Punkt zum anderen kommst. Den Vektor AB⃗ erhältst du, indem du die Koordinaten des Startpunkts A von denen des Zielpunkts B subtrahierst: AB⃗ = $b₁-a₁, b₂-a₂, b₃-a₃$.

💡 Merktipp: Bei Vektoren gilt immer "Ziel minus Start" - so wie beim Navigationsgerät!

Verschiedene Vektortypen und Rechnen

Gegenvektor und Ortsvektor sind zwei wichtige Spezialfälle. Der Gegenvektor -a⃗ entsteht, wenn du alle Vorzeichen umkehrst. Der Ortsvektor zeigt vom Ursprung zu einem Punkt - praktisch wie eine Adresse im Koordinatensystem.

Den Betrag eines Vektors berechnest du genauso wie den Abstand zwischen Punkten. Das gibt dir die "Länge" des Vektors an.

Kollineare Vektoren sind Vielfache voneinander und zeigen in dieselbe (oder entgegengesetzte) Richtung. Wenn a⃗ = r·b⃗ gilt, dann sind sie kollinear.

Linearkombinationen funktionieren super intuitiv: Du kannst Vektoren addieren (koordinatenweise) und mit Zahlen multiplizieren. Das ist wie Lego-Bausteine zusammensetzen - jede Koordinate wird einzeln behandelt.

💡 Praxistipp: Kollineare Vektoren erkennst du sofort, wenn alle Koordinaten das gleiche Vielfache haben!

Geraden im Raum

Eine Gerade beschreibst du mit der Formel g: x⃗ = p⃗ + r·u⃗. Das ist wie ein Rezept: Nimm einen festen Punkt (Stützvektor p⃗), gehe dann in eine bestimmte Richtung (Richtungsvektor u⃗) und variiere dabei die Schrittlänge (Parameter r).

Der Stützvektor ist ein beliebiger Punkt auf der Gerade, der Richtungsvektor gibt an, in welche Richtung die Gerade verläuft. Setzt du für r alle reellen Zahlen ein, erhältst du alle Punkte der Gerade.

Eine Gerade kann durch unendlich viele Gleichungen beschrieben werden! Die Richtungsvektoren müssen nur kollinear sein, und die Stützvektoren müssen auf der Gerade liegen.

Zum Zeichnen trägst du zuerst den Stützvektor ein, dann den Richtungsvektor vom Endpunkt des Stützvektors aus. Fertig ist deine Gerade!

💡 Visualisierungstrick: Stelle dir vor, du stehst am Stützpunkt und gehst immer weiter in Richtung des Richtungsvektors!

Lagebeziehungen von Geraden

Es gibt vier Möglichkeiten, wie sich zwei Geraden zueinander verhalten können. Das Geheimnis liegt in den Richtungsvektoren und Stützvektoren!

Identische Geraden: Die Richtungsvektoren sind kollinear UND der Stützvektor der einen liegt auf der anderen Gerade. Parallele Geraden: Richtungsvektoren sind kollinear, aber der Stützvektor liegt NICHT auf der anderen Gerade.

Schneidende Geraden: Richtungsvektoren sind nicht kollinear, und sie haben einen gemeinsamen Punkt. Windschiefe Geraden: Richtungsvektoren sind nicht kollinear UND sie haben keinen gemeinsamen Punkt - das gibt's nur im Raum!

Spurpunkte sind die Schnittpunkte einer Gerade mit den Koordinatenebenen. Du setzt eine Koordinate gleich null und löst nach dem Parameter r auf.

💡 Eselsbrücke: Windschief = "aneinander vorbei im Raum" - wie zwei Autobahnen auf verschiedenen Höhen!

Rechenmethoden für Geraden

Du willst wissen, ob ein Punkt auf einer Gerade liegt? Setze den Punkt in die Geradengleichung ein und löse das Gleichungssystem nach r auf. Gibt's eine eindeutige Lösung, liegt er drauf!

Für Schnittpunkte zweier Geraden prüfst du zuerst, ob die Richtungsvektoren nicht kollinear sind. Dann setzt du die Geradengleichungen gleich und löst das entstehende Gleichungssystem.

Das Gauß-Verfahren ist dein bester Freund bei größeren Gleichungssystemen. Du bringst die Matrix in Stufenform, indem du geschickt Zeilen addierst und subtrahierst. Am Ende liest du die Lösung von unten nach oben ab.

Die Beispielrechnungen zeigen dir Schritt für Schritt, wie's funktioniert. Mit etwas Übung wird das zur Routine!

💡 Strategietipp: Beim Gauß-Verfahren immer systematisch vorgehen - erst x₁ eliminieren, dann x₂, dann x₃!

Orthogonalität und Winkel

Orthogonalität bedeutet, dass zwei Vektoren senkrecht zueinander stehen (Symbol: a⃗ ⊥ b⃗). Das prüfst du mit dem Skalarprodukt: a⃗·b⃗ = a₁·b₁ + a₂·b₂ + a₃·b₃ = 0.

Das Skalarprodukt ist super praktisch - es multipliziert entsprechende Koordinaten und addiert alles auf. Kommt null raus, stehen die Vektoren senkrecht aufeinander.

Für den Winkel zwischen Vektoren nutzt du die Formel: cos(α) = (a⃗·b⃗)/(|a⃗|·|b⃗|). Das Skalarprodukt wird durch das Produkt der Beträge geteilt.

Bei Geraden verwendest du einfach ihre Richtungsvektoren für diese Berechnungen. So findest du heraus, ob Geraden senkrecht stehen oder welchen Winkel sie einschließen.

💡 Merkregel: Skalarprodukt = 0 bedeutet immer senkrecht (orthogonal)!

Ebenen im Raum

Eine Ebene beschreibst du am besten in Parameterform: E: x⃗ = p⃗ + r·u⃗ + s·v⃗. Du brauchst einen Stützvektor und zwei nicht-parallele Spannvektoren. Die Parameter r und s können alle reellen Zahlen annehmen.

Bei drei vorgegebenen Punkten nimmst du einen als Stützvektor und bildest die Verbindungsvektoren zu den anderen beiden als Spannvektoren. Fertig ist deine Ebenengleichung!

Die Normalengleichung nutzt einen Normalenvektor, der senkrecht zur Ebene steht: E: $x⃗ - p⃗$·n⃗ = 0. Der Normalenvektor steht orthogonal zu allen Vektoren in der Ebene.

Beide Darstellungen haben ihre Vorteile - die Parameterform ist anschaulich, die Normalengleichung praktisch für Rechnungen.

💡 Vorstellungshilfe: Eine Ebene ist wie ein unendlich großes Blatt Papier im Raum!

Koordinatengleichung und Normalenvektor

Die Koordinatengleichung hat die Form n₁x₁ + n₂x₂ + n₃x₃ = d. Die Koeffizienten n₁, n₂, n₃ sind die Koordinaten des Normalenvektors, d erhältst du durch das Skalarprodukt von Stützvektor und Normalenvektor.

Den Normalenvektor bestimmst du über Skalarprodukte: Er muss orthogonal zu beiden Spannvektoren sein. Das führt zu einem Gleichungssystem, das du löst.

Das Kreuzprodukt ist eine elegante Alternative: a⃗ × b⃗ = $a₂b₃-a₃b₂, a₃b₁-a₁b₃, a₁b₂-a₂b₁$. Das Ergebnis steht automatisch senkrecht auf beiden ursprünglichen Vektoren.

Beim Lösen des Gleichungssystems für den Normalenvektor wählst du eine Variable geschickt, damit schöne ganze Zahlen rauskommen.

💡 Rechentrick: Das Kreuzprodukt merkst du dir mit der "Schief-Formel" - jede Komponente entsteht aus den anderen beiden!

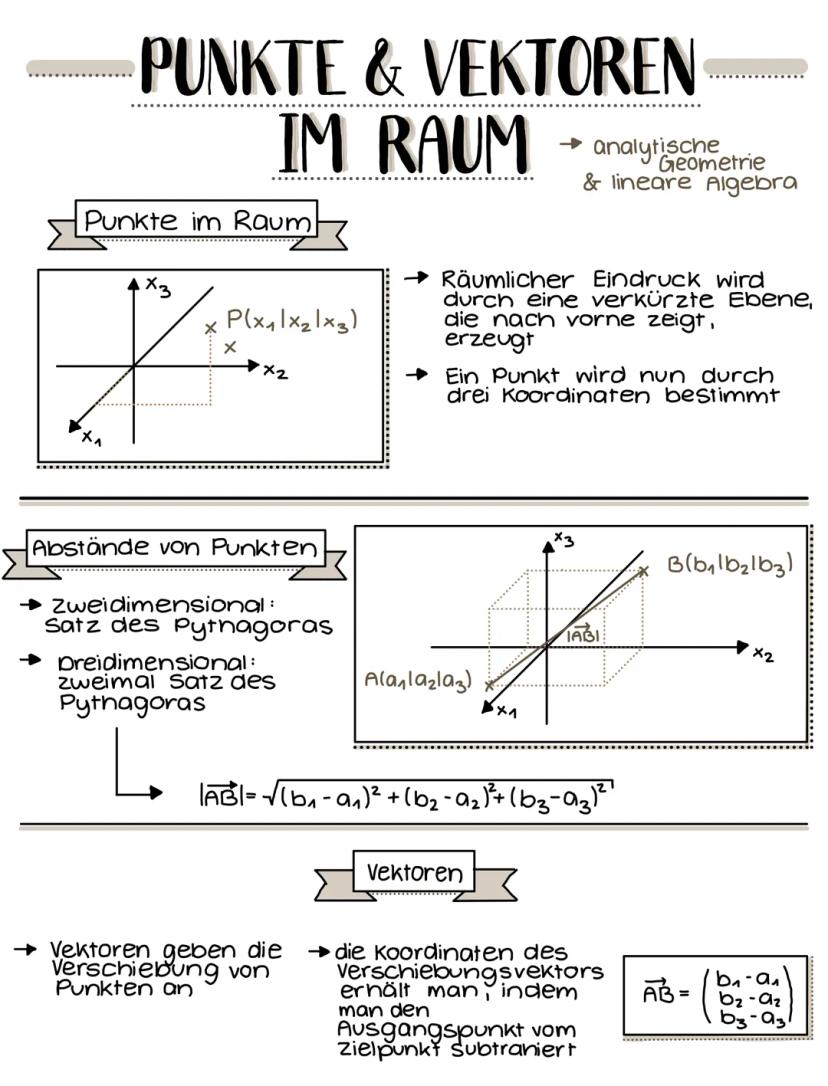
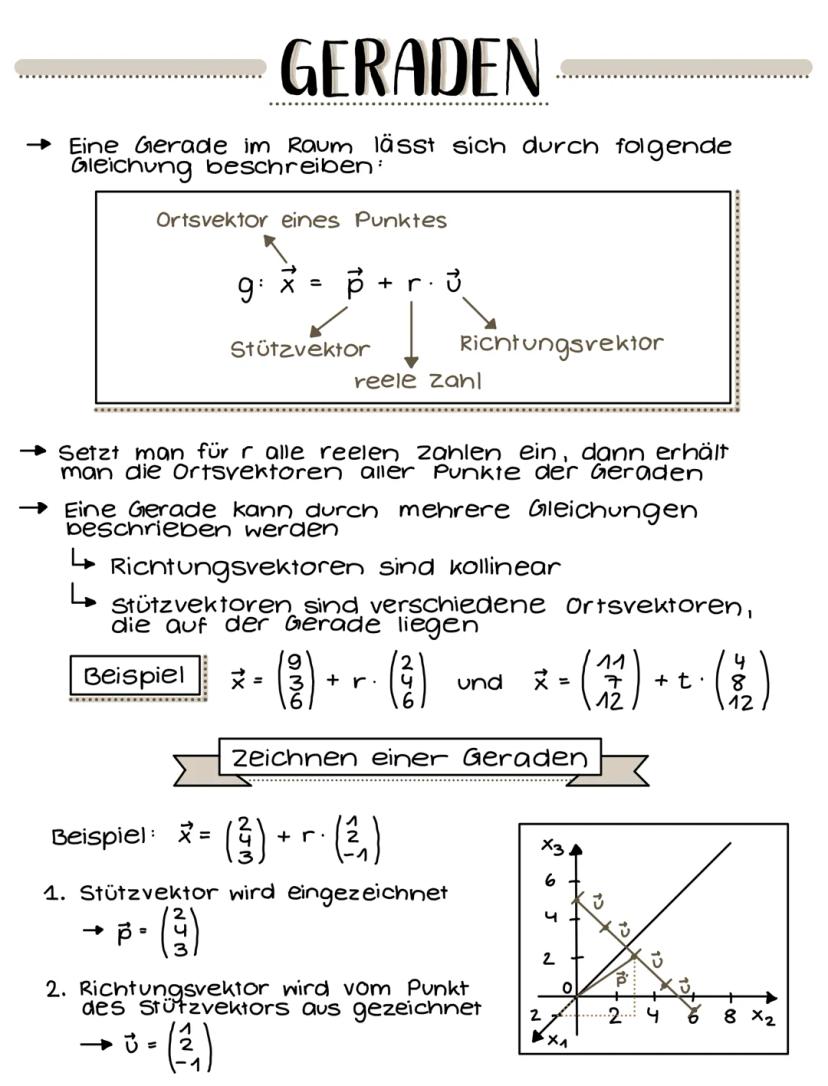
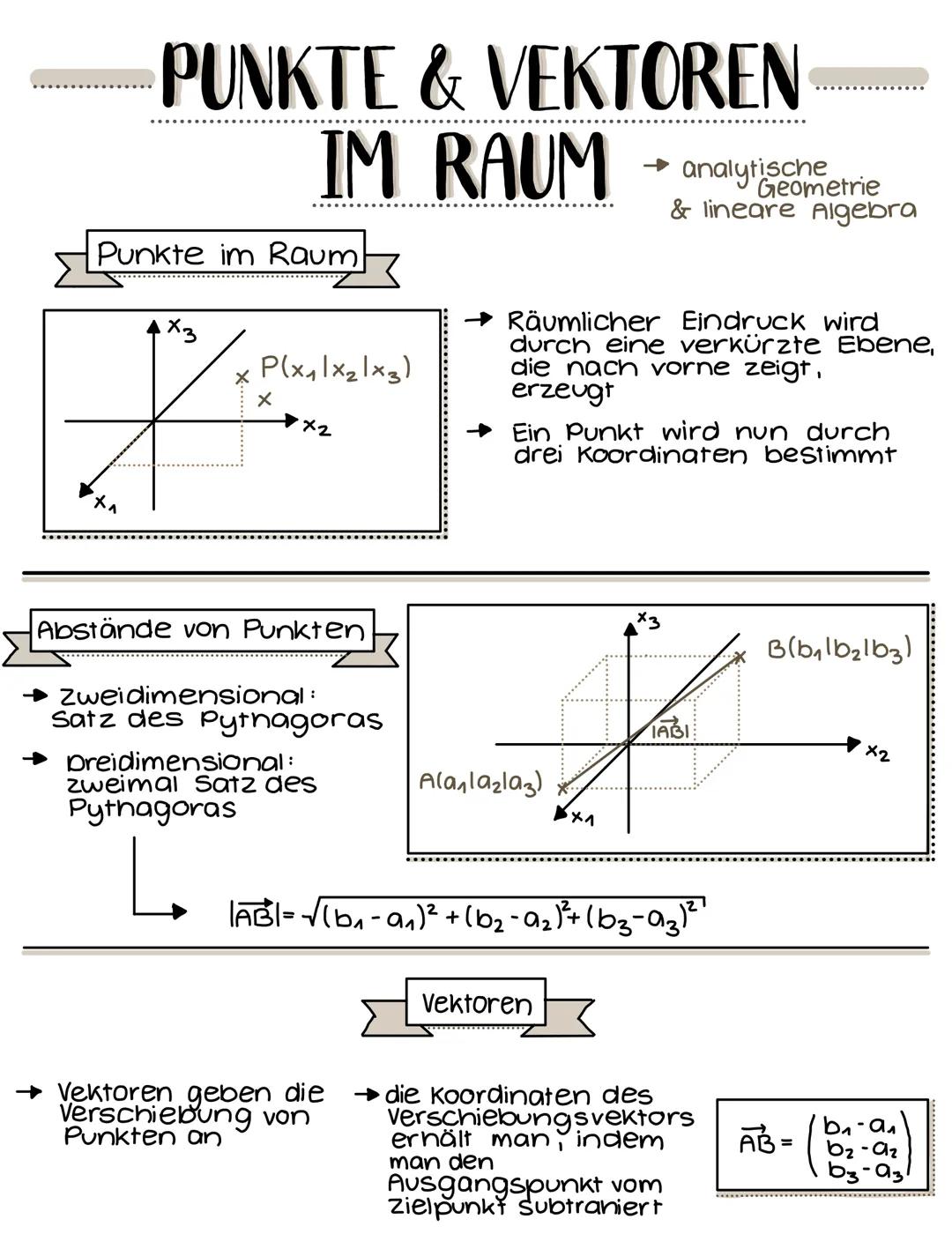
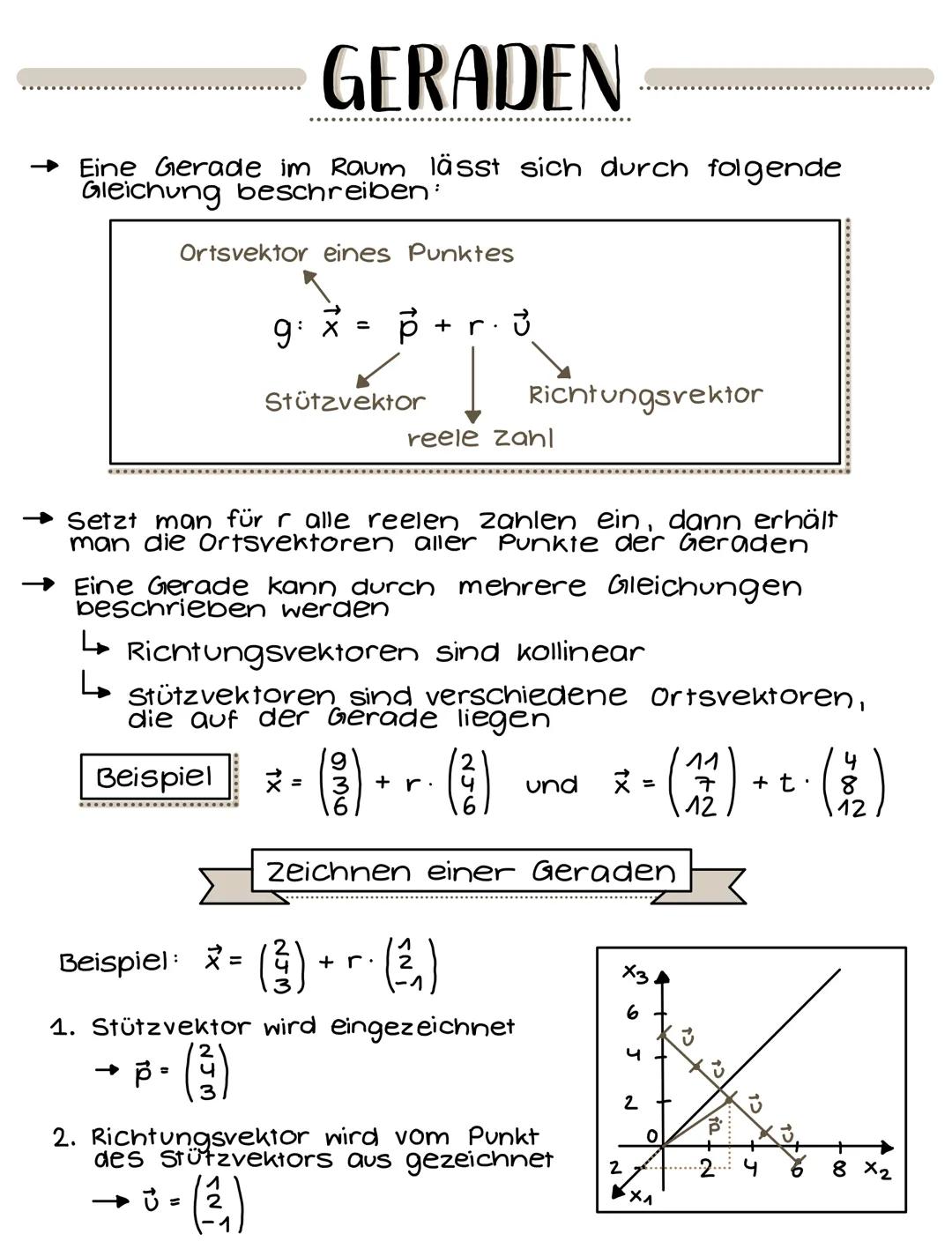
Lagebeziehungen Gerade-Ebene

Wenn sich Gerade und Ebene treffen, gibt's drei Möglichkeiten: Sie schneiden sich in einem Punkt, sind parallel oder die Gerade liegt komplett in der Ebene.

Bei der Parameterform setzt du die Geradengleichung in die Ebenengleichung ein und löst das entstehende Gleichungssystem. Eine Lösung = ein Schnittpunkt, keine Lösung = parallel, unendlich viele Lösungen = Gerade liegt in der Ebene.

Bei der Koordinatenform zerlegst du die Gerade in einzelne Koordinatengleichungen $x₁ = ..., x₂ = ..., x₃ = ...$ und setzt diese in die Ebenengleichung ein.

Das Beispiel zeigt's konkret: Du erhältst eine Gleichung mit nur noch dem Parameter t, löst diese auf und setzt t zurück in die Geradengleichung ein.

💡 Systematik: Immer erst prüfen, ob das Gleichungssystem lösbar ist - dann weißt du schon, welcher Fall vorliegt!

Abstände und praktische Anwendungen

Um zu prüfen, ob zwei Punkte auf derselben Seite einer Ebene liegen, stellst du eine Gerade durch beide Punkte auf. Schneidet diese die Ebene zwischen den Punkten (0 < t < 1), liegen sie auf verschiedenen Seiten.

Der Abstand Punkt-Ebene ist die kürzeste Entfernung. Du stellst eine Lotgerade auf (durch den Punkt mit Normalenvektor als Richtung), findest den Schnittpunkt mit der Ebene (Lotfußpunkt) und berechnest den Abstand zwischen Punkt und Lotfußpunkt.

Das Verfahren ist immer gleich: Normalenvektor bestimmen, Lotgerade aufstellen, Schnittpunkt berechnen, Abstand messen. Der Normalenvektor erhältst du aus dem Kreuzprodukt der Spannvektoren.

Diese Methoden sind fundamental für viele geometrische Probleme und kommen garantiert in der Klausur vor!

💡 Prüfungstipp: Der Lotfußpunkt ist immer der Punkt auf der Ebene, der dem gegebenen Punkt am nächsten liegt!